Current Electricity 4 Question 7
7. In the experimental set up of meter bridge shown in the figure, the null point is obtained at a distance of $40 cm$ from $A$. If a $10 \Omega$ resistor is connected in series with $R _1$, the null point shifts by $10 cm$.
The resistance that should be connected in parallel with $\left(R _1+10\right) \Omega$ such that the null point shifts back to its initial position is
(Main 2019, 11 Jan II)
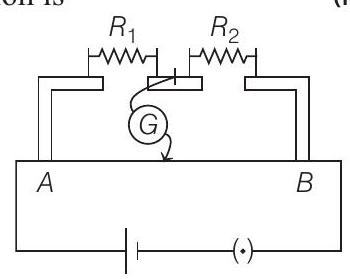
(a) $60 \Omega$
(b) $20 \Omega$
(c) $30 \Omega$
(d) $40 \Omega$
Show Answer
Solution:
- For meter bridge, if balancing length is $l cm$, then in first case, $\frac{R _1}{R _2}=\frac{l}{(100-l)}$
It is given that, $l=40 cm$,
$$ \begin{aligned} \text { So, } & \frac{R _1}{40} & =\frac{R _2}{100-40} \\ \text { or } & \frac{R _1}{R _2} & =\frac{2}{3} \end{aligned} $$
In second case, $R _1^{\prime}=R _1+10$, and balancing length is now $50 cm$ then
or
$$ \begin{gathered} \frac{R _1+10}{50}=\frac{R _2}{(100-50)} \\ R _1+10=R _2 \end{gathered} $$
Substituting value of $R _2$ from (ii) to (i) we get,
$$ \begin{aligned} \text { or } & \frac{R _1}{10+R _1} & =\frac{2}{3} \\ \Rightarrow & 3 R _1 & =20+2 R _1 \\ \text { or } & R _1 & =20 \Omega \\ \Rightarrow & R _2 & =30 \Omega \end{aligned} $$
Let us assume the parallel connected resistance is $x$.
Then equivalent resistance is $\frac{x\left(R _1+10\right)}{x+R _1+100}$
So, this combination should be again equal to $R _1$.
$$ \begin{array}{rlrl} & & \frac{\left(R _1+10\right) x}{R _1+10+x} & =R _1 \\ \Rightarrow & & \frac{30 x}{30+x} & =20 \\ \text { or } & 30 x & =600+20 x \\ \text { or } & x & =60 \Omega \end{array} $$
