Current Electricity 4 Question 10
10. A potentiometer wire
(2019 Main, 10 Jan I)
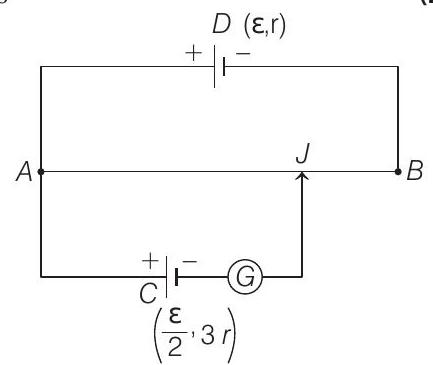
(a)
(b)
(c)
(d)
Show Answer
Solution:
- Given, length of potentiometer wire
Resistance of potentiometer wire
EMF of cell
Internal resistance of cell ’
EMF of cell ’
Internal resistance of cell ’
Current in potentiometer wire
Potential drop across the balance length
where,
As null point occurs at






