SATHEE: Current Electricity 3 Question 14

Current Electricity 3 Question 14

13. For the circuit shown in the figure

(2009)

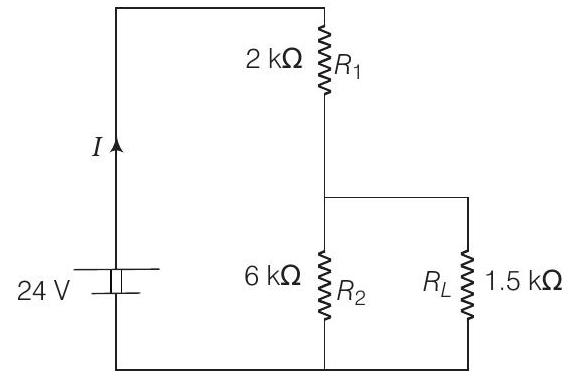
Show Answer

Solution:

$R_{total} = 2 + \frac{6 \times 1.5}{6 + 1.5} = 3.2 k Ω$

(a) $I = \frac{24 V}{3.2 k Ω} = 7.5 m A = I_{R_{1}}$

$I_{R_{2}} = \frac{R_{L}}{R_{L} + R_{2}} I$

$I = \frac{1.5}{7.5} \times 7.5 = 1.5 m A$

$I_{R_{L}} = 6 m A$

(b) $V_{R_{L}} = (I_{R_{L}}) (R_{L}) = 9 V$

(c) $\frac{P_{R_{1}}}{P_{R_{2}}} = \frac{(I_{R_{1}}^{2}) R_{1}}{(I_{R_{2}}^{2}) R_{2}} = \frac{(7.5)^{2} (2)}{(1.5)^{2} (6)} = \frac{25}{3}$

(d) When $R_{1}$ and $R_{2}$ are inter changed, then

$\frac{R_{2} R_{L}}{R_{2} + R_{L}} = \frac{2 \times 1.5}{3.5} = \frac{6}{7} k Ω$

Now potential difference across $R_{L}$ will be

$V_{L} = 24 \frac{6 / 7}{6 + 6 / 7} = 3 V$

Earlier it was $9 V$

Since, $P = \frac{V^{2}}{R}$ or $P \propto V^{2}$

In new situation potential difference has been decreased three times. Therefore, power dissipated will decrease by a factor of 9.

पिछला

अगला

गोपनीयता नीति

द्वारा संचालित Prutor@IITK

sathee@iitk.ac.in

SATHEE का मीडिया कवरेज

खेल स्टोर

ऐप स्टोर

Ask SATHEE

Welcome to SATHEE !
Select from 'Menu' to explore our services, or ask SATHEE to get started. Let's embark on this journey of growth together! 🌐📚🚀🎓

I'm relatively new and can sometimes make mistakes.
If you notice any error, such as an incorrect solution, please use the thumbs down icon to aid my learning.
To begin your journey now, click on "I understand".

Current Electricity 3 Question 14

13. For the circuit shown in the figure

Solution:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu