Current Electricity 2 Question 9
9. In the given circuit, the internal resistance of the $18 V$ cell is negligible. If $R _1=400 \Omega, R _3=100 \Omega$ and $R _4=500 \Omega$ and the reading of an ideal voltmeter across $R _4$ is $5 V$, then the value of $R _2$ will be
(2019 Main, 9 Jan II)
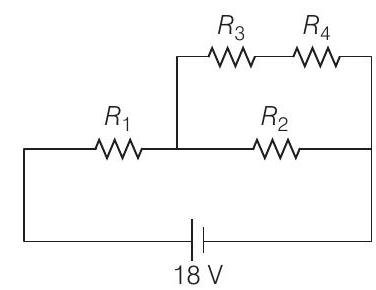
(a) $550 \Omega$
(b) $230 \Omega$
(c) $300 \Omega$
(d) $450 \Omega$
Show Answer
Solution:
- According to question, the voltage across $R _4$ is 5 volt, then the current across it
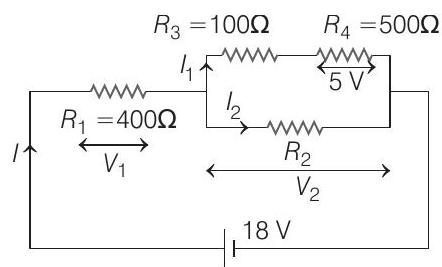
According to Ohm’s law,
$$ \begin{gathered} \Rightarrow \quad V=I R \quad \Rightarrow \quad 5=I _1 \times R _4 \\ \Rightarrow \quad 5=I _1 \times 500 \\ \\ I _1=\frac{5}{500}=\frac{1}{100} A \end{gathered} $$
The potential difference across series combination of $R _3$ and $R _4$
$\Rightarrow \quad V _2=\left(R _3+R _4\right) I=600 \times \frac{1}{100}=6$ Volt
So, potential difference (across $R _1$ )
$$ V _1=18-6=12 V $$
Current through $R _1$ is,
$$ I=\frac{V _1}{R _1}=\frac{12}{400}=\frac{3}{100} A $$
So current through $R _2$ is,
$$ I _2=I-I _1=\frac{3}{100}-\frac{1}{100} A=\frac{2}{100} A $$
Now, from $V=I R$, we have,
$$ R _2=\frac{V _2}{I _2}=\frac{6}{(2 / 100)}=300 \Omega $$
