Current Electricity 2 Question 6
6. In a Wheatstone bridge (see figure), resistances
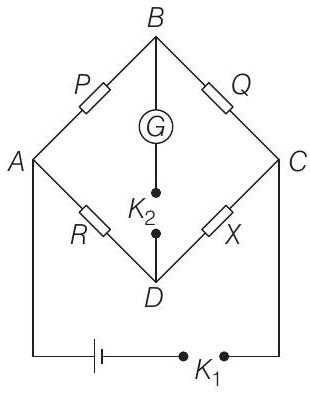
(2019 Main, 11 Jan I)
(a)
(b)
(c)
(d)
Show Answer
Solution:
- For a balanced Wheatstone bridge,
In first case when
In second case,
Substituting the value of
The value of






