SATHEE: Current Electricity 2 Question 27

Current Electricity 2 Question 27

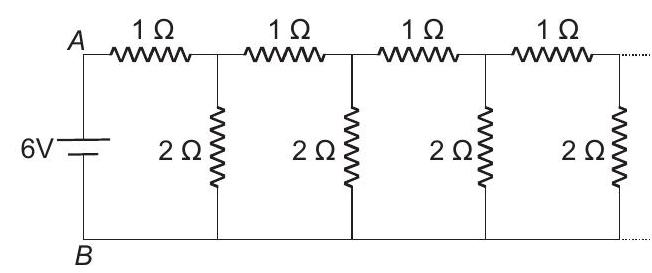
27. An infinite ladder network of resistances is constructed with $1 Ω$ and $2 Ω$ resistances, as shown in figure.

The $6 V$ battery between $A$ and $B$ has negligible internal resistance.

(1987, 7M)

(a) Show that the effective resistance between $A$ and $B$ is $2 Ω$ .

(b) What is the current that passes through the $2 Ω$ resistance nearest to the battery?

Show Answer

Solution:

(a) Let $R_{A B} = x$ . Then, we can break one chain and connect a resistance of magnitude $x$ in place of it.

Thus, the circuit remains as shown in figure.

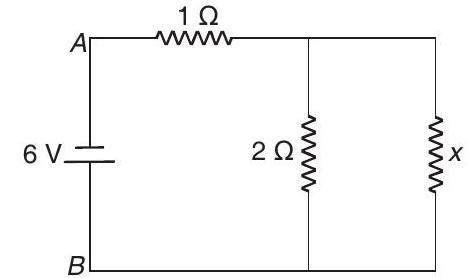
Now, $2 x$ and $x$ are in parallel. So, their combined resistance is $\frac{2 x}{2 + x}$

$or R_{A B} = 1 + \frac{2 x}{2 + x}$

But $R_{A B}$ is assumed as $x$ . Therefore,

$x = 1 + \frac{2 x}{2 + x}$

Solving this equation, we get

$x = 2 Ω$

Hence proved.

(b) Net resistance of circuit $R = 1 + \frac{2 \times 2}{2 + 2} = 2 Ω$

$∴$ Current through battery $i = \frac{6}{2} = 3 A$

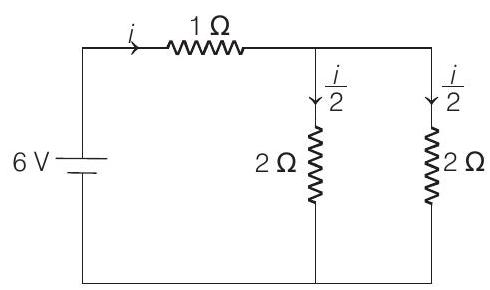
This current is equally distributed in $2 Ω$ and $2 Ω$ resistances. Therefore, the desired current is $\frac{i}{2}$ or $1.5 A$ .

पिछला

अगला

Current Electricity 2 Question 27

27. An infinite ladder network of resistances is constructed with $1 Ω$ and $2 Ω$ resistances, as shown in figure.

Solution:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Current Electricity 2 Question 27

27. An infinite ladder network of resistances is constructed with 1Ω and 2Ω resistances, as shown in figure.

Solution:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu

27. An infinite ladder network of resistances is constructed with $1 Ω$ and $2 Ω$ resistances, as shown in figure.