Current Electricity 2 Question 15
15. In the given circuit, it is observed that the current
(2001, 2M)
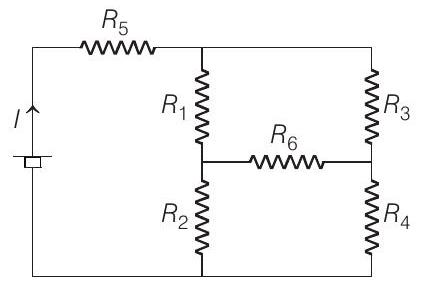
(a)
(b)
(c)
(d)
Show Answer
Solution:
- Current
Therefore,






