Current Electricity 1 Question 6
6. Determine the charge on the capacitor in the following circuit
(2019 Main, 9 April I)
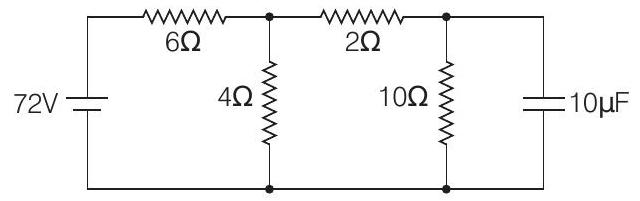
(a)
(b)
(c)
(d)
Show Answer
Solution:
- Given circuit is
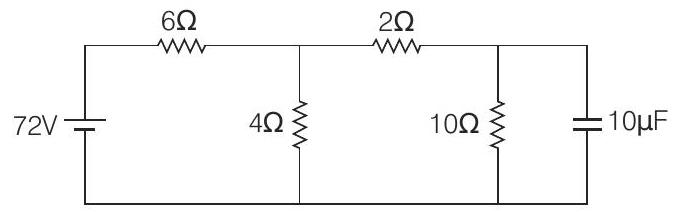
To find charge on capacitor, we need to determine voltage across it. In steady state, capacitor will acts as open circuit and circuit can be reduced as
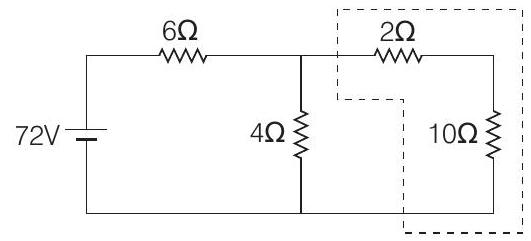
In series,
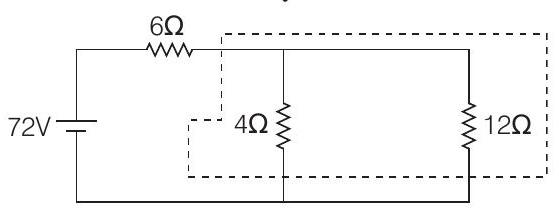
In parallel,
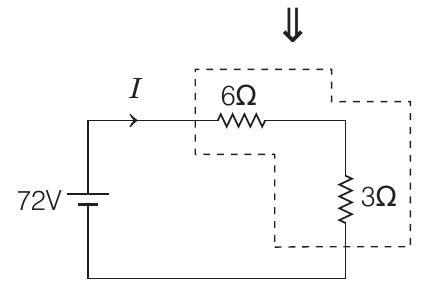
In series,
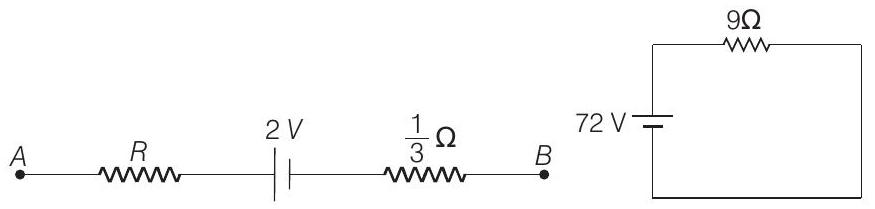
So, current in steady state,
Now, by using current division, at point
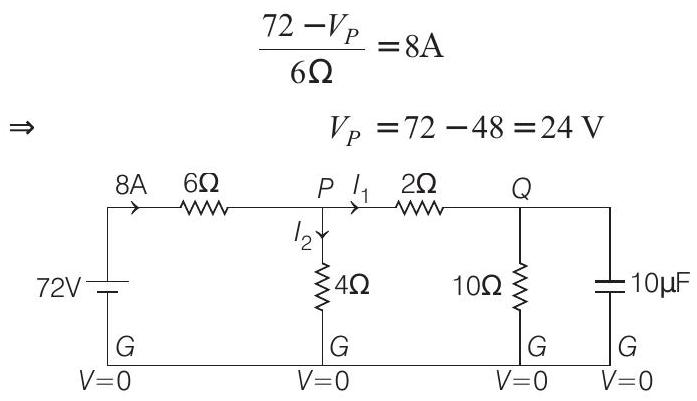
Current in
So, current in
Same potential difference will be applicable over the capacitor (parallel combination).
So, charge stored in the capacitor will be






