SATHEE: Current Electricity 1 Question 4

Current Electricity 1 Question 4

4. A metal wire of resistance $3 Ω$ is elongated to make a uniform wire of double its previous length. This new wire is now bent and the ends joined to make a circle. If two points on this circle make an angle $60^{\circ}$ at the centre, the equivalent resistance between these two points will be

(Main 2019, 9 April II)

(a) $\frac{7}{2} Ω$

(b) $\frac{5}{2} Ω$

(d) $\frac{5}{3} Ω$

Show Answer

Solution:

Initial resistance of wire is $3 Ω$ . Let its length is $l$ and area is $A$ .

Then, $R_{initial} = ρ \frac{l}{A} = 3 Ω$

When wire is stretched twice its length, then its area becomes $A^{'}$ , on equating volume, we have

$A l = A^{'} 2 l \Rightarrow A^{'} = \frac{A}{2}$

So, after stretching, resistance of wire will be

$R^{'} = R_{final} = ρ \frac{l^{'}}{A^{'}} = 4 ρ \frac{l}{A} = 12 Ω [using Eq. (i)]$

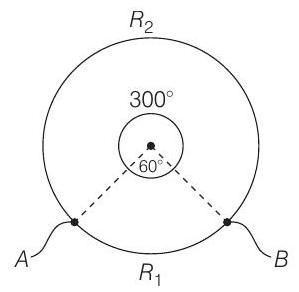
Now, this wire is made into a circle and connected across two points $A$ and $B$ (making $60^{\circ}$ angle at centre) as

Now, above arrangement is a combination of two resistances in parallel,

$\begin{aligned} R_{1} = \frac{60 \times R^{'}}{360} = \frac{1}{6} \times 12 = 2 Ω \\ and R_{2} = \frac{300}{360} \times R^{'} = \frac{5}{6} \times 12 = 10 Ω \end{aligned}$

Since, $R_{1}$ and $R_{2}$ are connected in parallel.

So, $R_{A B} = \frac{R_{1} R_{2}}{R_{1} + R_{2}} = \frac{10 \times 2}{12} = \frac{5}{3} Ω$

पिछला

अगला

Current Electricity 1 Question 4

4. A metal wire of resistance $3 Ω$ is elongated to make a uniform wire of double its previous length. This new wire is now bent and the ends joined to make a circle. If two points on this circle make an angle $60^{\circ}$ at the centre, the equivalent resistance between these two points will be

Solution:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Current Electricity 1 Question 4

4. A metal wire of resistance 3Ω is elongated to make a uniform wire of double its previous length. This new wire is now bent and the ends joined to make a circle. If two points on this circle make an angle 60∘ at the centre, the equivalent resistance between these two points will be

Solution:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu

4. A metal wire of resistance $3 Ω$ is elongated to make a uniform wire of double its previous length. This new wire is now bent and the ends joined to make a circle. If two points on this circle make an angle $60^{\circ}$ at the centre, the equivalent resistance between these two points will be