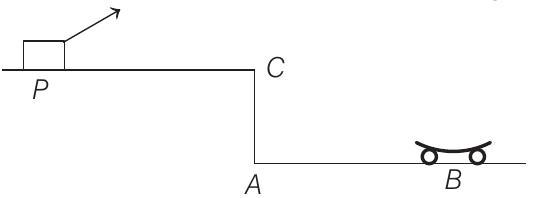
Centre of Mass 4 Question 7
8. A car $P$ is moving with a uniform speed of $5 \sqrt{3} m / s$ towards a carriage of mass $9 kg$ at rest kept on the rails at a point $B$ as shown in figure. The height $A C$ is $120 m$. Cannon balls of $1 kg$ are fired from the car with an initial velocity $100 m / s$ at an angle $30^{\circ}$ with the horizontal. The first cannon ball hits the stationary carriage after a time $t _0$ and sticks to it. Determine $t _0$. At $t _0$, the second cannon ball is fired. Assume that the resistive force between the rails and the carriage is constant and ignore the vertical motion of the carriage throughout.
If the second ball also hits and sticks to the carriage, what will be the horizontal velocity of the carriage just after the second impact?
(2011, 10M)
Show Answer
Answer:
Correct Answer: 8. $12 s, 15.75 m / s$
Solution:
- (a) $100 m / s$ velocity of the ball is relative to ground.
[Unless and until it is mentioned in the question, the velocity is always relative to ground]
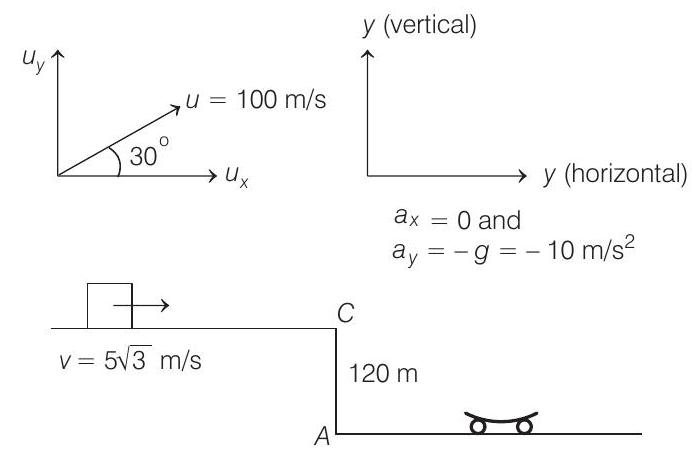
Horizontal component of velocity of cannon ball,
or
$$ \begin{aligned} & u _x=u \cos 30^{\circ} \\ & u _x=(100) \times \frac{\sqrt{3}}{2}=50 \sqrt{3} m / s \end{aligned} $$
and vertical component of its velocity,
$$ \begin{aligned} & u _y=u \sin 30^{\circ} \\ & u _y=100 \times \frac{1}{2}=50 m / s \end{aligned} $$
Vertical displacement of the ball when it strikes the carriage is $-120 m$ or
$$ \begin{aligned} & s _y=u _y t+\frac{1}{2} a _y t^{2} \Rightarrow-120=(50 t)+\frac{1}{2}(-10) t^{2} \\ & \Rightarrow t^{2}-10 t-24=0 \Rightarrow t=12 s \text { or }-2 s \end{aligned} $$
Ignoring the negative time, we have
$$ t _0=12 s $$
(b) When it strikes the carriage, its horizontal component of velocity is still $50 \sqrt{3} m / s$. It strikes to the carriage. Let $v _2$ be the velocity of (carriage + ball) system after collision. Then, applying conservation of linear momentum in horizontal direction
(mass of ball) (horizontal component of its velocity before collision $)=($ mass of ball + carriage $)\left(v _2\right)$
$$ \begin{aligned} & \therefore & (1 kg)(50 \sqrt{3} m / s) & =(10 kg)\left(v _2\right) \\ & \therefore & v _2 & =5 \sqrt{3} m / s \end{aligned} $$
The second ball is fired when the first ball strikes the carriage i.e. after $12 s$. In these $12 s$, the car will move forward a distance of $12 v _1$ or $60 \sqrt{3} m$.
The second ball also takes $12 s$ to travel a vertical displacement of $-120 m$. This ball will strike the carriage only when the carriage also covers the same distance of $60 \sqrt{3} m$ in these $12 s$. This is possible only when resistive forces are zero because velocity of car $\left(v _1\right)=$ velocity of carriage after first collision. $\left(v _2\right)=5 \sqrt{3} m / s$. Hence, at the time of second collision
Horizontal component of velocity of ball $=50 \sqrt{3} m / s$ and horizontal velocity of carriage + first ball $=5 \sqrt{3} m / s$. Let $v$ be the desired velocity of carriage after second collision. Then, conservation of linear momentum in horizontal direction gives
$$ \begin{aligned} 11 v & =(1)(50 \sqrt{3})+(10)(5 \sqrt{3}) \\ & =100 \sqrt{3} \\ \therefore \quad v & =\frac{100 \sqrt{3}}{11} m / s \\ \text { or } \quad v & =15.75 m / s \end{aligned} $$
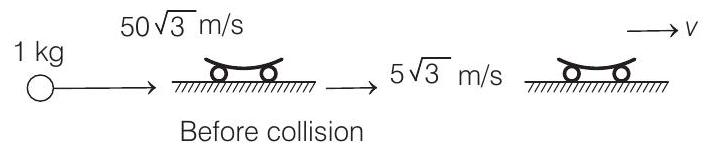
In this particular problem, values are so adjusted that even if we take the velocity of ball with respect to car, we get the same results of both the parts, although the method will be wrong.
