Centre of Mass 4 Question 3
4. A particle of mass $m$ is moving along the side of a square of side $a$, with a uniform speed $v$ in the $x y$-plane as shown in the figure.
(2016 Main)
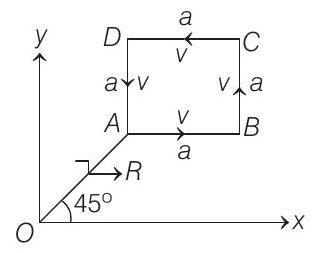
Which of the following statements is false for the angular momentum $\mathbf{L}$ about the origin?
(a) $\mathbf{L}=\frac{-m v}{\sqrt{2}} R \hat{\mathbf{k}}$ when the particle is moving from $A$ to $B$
(b) $\mathbf{L}=m v \frac{R}{\sqrt{2}}-a \hat{\mathbf{k}}$ when the particle is moving from
$C$ to $D$
(c) $\mathbf{L}=m v \frac{R}{\sqrt{2}}+a \hat{\mathbf{k}}$ when the particle is moving from $B$
to $C$
(d) $\mathbf{L}=\frac{m v}{\sqrt{2}} R \hat{\mathbf{k}}$ when the particle is moving from $D$ to $A$
Numerical Value
Show Answer
Answer:
Correct Answer: 4. (b, d)
Solution:
- We can apply $\mathbf{L}=m(\mathbf{r} \times \mathbf{v})$ for different parts.
For example :
In part (a), coordinates of $A$ are $\frac{R}{\sqrt{2}}, \frac{R}{\sqrt{2}}$ Therefore, $\quad \mathbf{r}=\frac{R}{\sqrt{2}} \hat{\mathbf{i}}+\frac{R}{\sqrt{2}} \hat{\mathbf{j}}$ and $\mathbf{v}=v \hat{\mathbf{i}}$
So, substituting in $\quad \mathbf{L}=m(\mathbf{r} \times \mathbf{v})$ we get,
$$ \mathbf{L}=-\frac{m v R}{\sqrt{2}} \hat{\mathbf{k}} $$
Hence, option (a) is correct. Similarly, we can check other options also.
