SATHEE: Centre of Mass 3 Question 7

Centre of Mass 3 Question 7

10. Three blocks $A, B$ and $C$ are lying on a smooth horizontal surface as shown in the figure. $A$ and $B$ have equal masses $m$ while $C$ has mass $M$ . Block $A$ is given an initial speed $v$ towards $B$ due to which it collides with $B$ perfectly inelastically. The combined mass collides with $C$ , also perfectly inelastically $\frac{5}{6}$ th of the initial kinetic energy is lost in whole process. What is value of $\frac{M}{m}$ ?

(2019 Main, 9 Jan I)

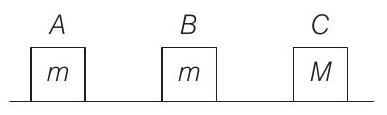
(a) 4

(b) 2

(d) 5

Show Answer

Answer:

Correct Answer: 10. (a)

Solution:

Key Idea For a perfectly inelastic collision, the momentum of the system remains conserved but there is some of loss of kinetic energy. Also, after collision the objects of the system are stuck to each other and move as a combined system.

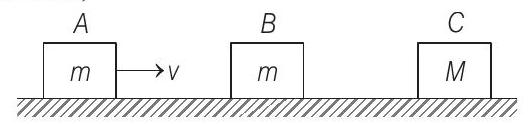
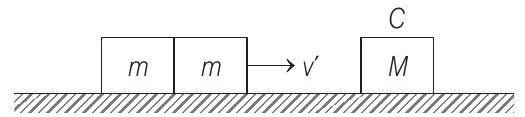
Initially, block $A$ is moving with velocity $v$ as shown in the figure below,

Now, $A$ collides with $B$ such that they collide inelastically. Thus, the combined mass (say) move with the velocity ’ $v$ ’ as shown below,

Then, if this combined system is collided inelastically again with the block $C$ .

So, now the velocity of system be $v^{''}$ as shown below.

Thus, according to the principle of conservation of momentum,

initial momentum of the system

$=$ final momentum of the system

$\begin{array}{ll} \Rightarrow & m v = (2 m + M) v^{''} \\ or & v^{''} = \frac{m v}{2 m + M} \end{array}$

Initial kinetic energy of the system,

$(K E)_{i} = \frac{1}{2} m v^{2}$

Final kinetic energy of the system, $(K E)_{f}$

$= \frac{1}{2} (2 m + M) {(v^{''})}^{2}$

$\begin{aligned} = \frac{1}{2} (2 m + M) \frac{m v}{2 m + M} \\ = \frac{1}{2} \cdot \frac{v^{2} m^{2}}{(2 m + M)} \end{aligned}$

Dividing Eq. (iii) and Eq. (ii), we get

$\frac{(K E)_{f}}{(K E)_{i}} = \frac{\frac{1}{2} m^{2} v^{2}}{\frac{(2 m + M)}{\frac{1}{2} m v^{2}}} = \frac{m}{2 m + M}$

It is given that $\frac{5}{6}$ th of $(K E)_{i}$ is lost in this process.

$\begin{aligned} \Rightarrow (K E)_{f} = \frac{1}{6} (K E)_{i} \\ \Rightarrow \frac{(K E)_{f}}{(K E)_{i}} = \frac{1}{6} \end{aligned}$

Comparing Eq. (iv) and Eq. (v), we get

$\begin{aligned} \frac{m}{2 m + M} = \frac{1}{6} \Rightarrow 6 m = 2 m + M \\ 4 m = M \Rightarrow \frac{M}{m} = 4 \end{aligned}$

पिछला

अगला

Centre of Mass 3 Question 7

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Centre of Mass 3 Question 7

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu