SATHEE: Centre of Mass 3 Question 4

Centre of Mass 3 Question 4

4. A body of mass $2 k g$ makes an elastic collision with a second body at rest and continues to move in the original direction but with one-fourth of its original speed. What is the mass of the second body?

(2019 Main, 9 April I)

(a) $1.5 k g$

(b) $1.2 k g$

(d) $1.0 k g$

Show Answer

Answer:

Correct Answer: 4. (b)

Solution:

Key Idea For an elastic collision, coefficient of restitution (e), i.e. the ratio of relative velocity of separation after collision to the relative velocity of approach before collision is 1 .

Given, mass of small body, $m = 2 k g$

Given situation is as shown

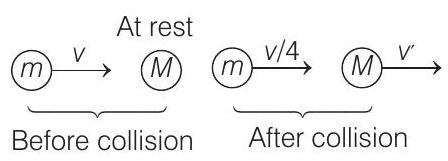
Using momentum conservation law for the given system, (Total momentum)

(Total momentum $)_{after collision}$

$\Rightarrow m (v) + M (0) = m \frac{v}{4} + M (v^{'}) \dots (i)$

$∵ e = 1$ and we know that,

$\begin{aligned} e & = - \frac{v_{2} - v_{1}}{u_{2} - u_{1}} \\ \Rightarrow & 1 & = - \frac{v^{'} - v / 4}{0 - v} \\ \Rightarrow & v & = v^{'} - v / 4 \\ or & v^{'} & = 5 v / 4 \end{aligned}$

Using value from Eq. (ii) into Eq. (i), we get

$\begin{aligned} m v = \frac{m v}{4} + M \frac{5 v}{4} \\ \Rightarrow m v - \frac{v}{4} = M \frac{5 v}{4} \\ \Rightarrow \frac{3}{4} m v = \frac{5}{4} M v \\ M = \frac{3}{5} m = \frac{3}{5} \times 2 = 1.2 k g \end{aligned}$

Key Idea Total linear momentum is conserved in all collisions, i.e. the initial momentum of the system is equal to final momentum of the system.

Given,

$m_{2} = 0.5 m_{1} \Rightarrow m_{1} = 2 m_{2}$

Let $m_{2} = m$ , then, $m_{1} = 2 m$

Also, $v_{3} = 0.5 v_{1}$

Given situation of collinear collision is as shown below Before collision,

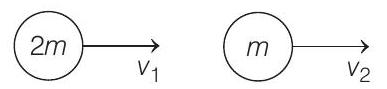
After collision,

$∴$ According to the conservation of linear momentum, Initial momentum $=$ Final momentum

$\begin{aligned} m_{1} v_{1} \hat{i} + m_{2} v_{2} \hat{i} = m_{1} v_{3} \hat{i} + m_{2} v_{4} \hat{i} \\ \Rightarrow 2 m v_{1} \hat{i} + m v_{2} \hat{i} = 2 m (0.5 v_{1}) \hat{i} + m v_{4} \hat{i} \\ \Rightarrow v_{4} = v_{1} + v_{2} \Rightarrow v_{1} = v_{4} - v_{2} \end{aligned}$