Centre of Mass 3 Question 34
37. A body of mass $1 kg$ initially at rest, explodes and breaks into three fragments of masses in the ratio $1: 1: 3$. The two pieces of equal mass fly-off perpendicular to each other with a speed of $30 m / s$ each. What is the velocity of the heavier fragment?
(1981, 3M)
Show Answer
Answer:
Correct Answer: 37. $10 \sqrt{2} m / s$ at $45^{\circ}$
Solution:
- From conservation of linear momentum $\mathbf{p} _3$ should be equal and opposite to $\mathbf{p} _{12}$ (resultant of $\mathbf{p} _1$ and $\mathbf{p} _2$ ). So, let $v^{\prime}$ be the velocity of third fragment, then
$$ (3 m) v^{\prime}=\sqrt{2} m v \quad \Rightarrow \quad \therefore \quad v^{\prime}=\frac{\sqrt{2}}{3} v $$
Here, $v=30 m / s$ (given) $\Rightarrow v^{\prime}=\frac{\sqrt{2}}{3} \times 30=10 \sqrt{2} m / s$
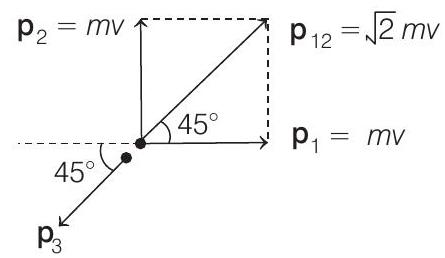
This velocity is at $45^{\circ}$ as shown in figure.
