Centre of Mass 3 Question 32
35. A simple pendulum is suspended from a peg on a vertical wall. The wall to a horizontal position (see fig.) and released. The ball hits the wall, the coefficient of restitution being $\frac{2}{\sqrt{5}}$. What is the minimum number of
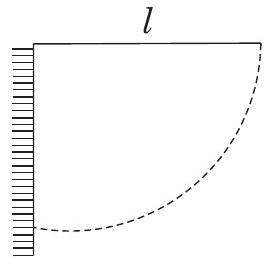collisions after which the amplitude of oscillations becomes less than 60 degrees?
$(1987,7$ M)
Show Answer
Answer:
Correct Answer: 35. 4
Solution:
- As shown in figure initially when the bob is at $A$, its potential energy is $m g l$. When the bob is released and it strikes the wall at $B$, its potential energy $m g l$ is converted into its kinetic energy. If $v$ be the velocity with which the bob strikes the wall, then
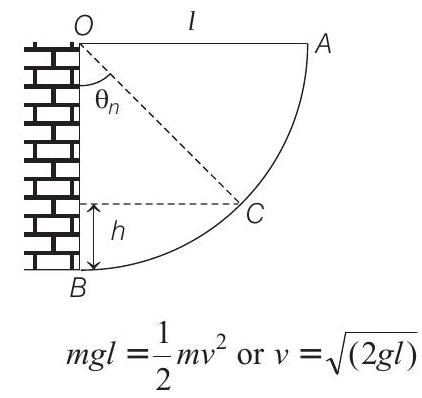
Speed of the bob after rebounding (first time)
$$ v _1=e \sqrt{(2 g l)} $$
The speed after second rebound is $v _2=e^{2} \sqrt{(2 g l)}$
In general after $n$ rebounds, the speed of the bob is
$$ v _n=e^{n} \sqrt{(2 g l)} $$
Let the bob rises to a height $h$ after $n$ rebounds. Applying the law of conservation of energy, we have
$\frac{1}{2} m v _n^{2}=m g h$
$\therefore \quad h=\frac{v _n^{2}}{2 g}=\frac{e^{2 n} \cdot 2 g l}{2 g}=e^{2 n} \cdot l=\frac{2}{\sqrt{5}}^{2 n} \cdot l=\frac{4}{5}^{n} l$
If $\theta _n$ be the angle after $n$ collisions, then
…(v)
$$ h=l-l \cos \theta _n=l\left(1-\cos \theta _n\right) $$
From Eqs. (iv) and (v), we have
$$ \frac{4}{5}^{n} l=l\left(1-\cos \theta _n\right) \text { or } \frac{4}{5}^{n}=\left(1-\cos \theta _n\right) $$
For $\theta _n$ to be less than $60^{\circ}$, i.e. $\cos \theta _n$ is greater than $1 / 2$, i.e. $\left(1-\cos \theta _n\right)$ is less than $1 / 2$, we have
$$ \frac{4}{5}^{n}<\frac{1}{2} $$
This condition is satisfied for $n=4$.
$\therefore$ Required number of collisions $=4$.
