SATHEE: Centre of Mass 3 Question 30

Centre of Mass 3 Question 30

33. A block $A$ of mass $2 m$ is placed on another block $B$ of mass $4 m$ which in turn is placed on a fixed table. The two blocks have a same length $4 d$ and they are placed as shown in figure. The coefficient of friction (both static and kinetic) between the block $B$ and table is $μ$ . There is no friction between the two blocks. A small object of mass $m$ moving horizontally along a line passing through the centre of mass (CM) of the block $B$ and perpendicular to its face with a speed $v$ collides elastically with the block $B$ at a height $d$ above the table.

(1991, $4 + 4$ M)

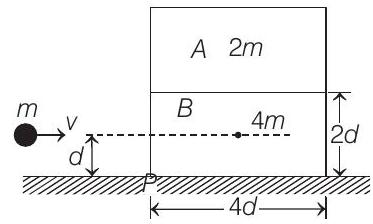
(a) What is the minimum value of $v$ (call it $v_{0}$ ) required to make the block $A$ to topple?

(b) If $v = 2 v_{0}$ , find the distance (from the point $P$ in the figure) at which the mass $m$ falls on the table after collision. (Ignore the role of friction during the collision.)

Show Answer

Answer:

Correct Answer: 33. (a) $\frac{5}{2} \sqrt{6 μ g d}$

(b) $6 d \sqrt{3 μ}$

Solution:

If $v_{1}$ and $v_{2}$ are the velocities of object of mass $m$ and block of mass $4 m$ , just after collision then by conservation of momentum,

$m v = m v_{1} + 4 m v_{2}, i.e. v = v_{1} + 4 v_{2}$

Further, as collision is elastic

$\frac{1}{2} m v^{2} = \frac{1}{2} m v_{1}^{2} + \frac{1}{2} 4 m v_{2}^{2}, i.e. v^{2} = v_{1}^{2} + 4 v_{2}^{2}$

Solving, these two equations we get either

Therefore, $v_{2} = \frac{2}{5} v$

$v_{2} = 0 or v_{2} = \frac{2}{5} v$

Substituting in Eq. (i) $v_{1} = \frac{3}{5} v$

when $v_{2} = 0, v_{1} = v_{2}$ , but it is physically unacceptable.

(a) Now, after collision the block $B$ will start moving with velocity $v_{2}$ to the right. Since, there is no friction between blocks $A$ and $B$ , the upper block $A$ will stay at its position and will topple if $B$ moves a distance $s$ such that

$s > 2 d$

However, the motion of $B$ is retarded by frictional force $f = μ (4 m + 2 m) g$ between table and its lower surface. So, the distance moved by $B$ till it stops

$0 = v_{2}^{2} - 2 \frac{6 μ m g}{4 m} s, i.e. s = \frac{v_{2}^{2}}{3 μ g}$

Substituting this value of $s$ in Eq. (iii), we find that for toppling of $A$

$\begin{aligned} v_{2}^{2} > 6 μ g d \\ \frac{2}{5} v > \sqrt{6 μ g d} [as v_{2} = 2 v / 5] \end{aligned}$

$\begin{aligned} i.e. & v > \frac{5}{2} \sqrt{6 μ g d} \\ or & v_{min} = v_{0} = \frac{5}{2} \sqrt{6 μ g d} \end{aligned}$

(b) If $v = 2 v_{0} = 5 \sqrt{6 μ g d}$ , the object will rebound with speed $v_{1} = \frac{3}{5} v = 3 \sqrt{6 μ g d}$ and as time taken by it to fall down

$t = \sqrt{\frac{2 h}{g}} = \sqrt{\frac{2 d}{g}} [as h = d]$

The horizontal distance moved by it to the left of $P$ in this time $x = v_{1} t = 6 d \sqrt{3 μ}$

NOTE

Toppling will take place if line of action of weight does not pass through the base area in contact.
$v_{1}$ and $v_{2}$ can be obtained by using the equations of head on elastic collision

$\begin{aligned} v_{1}^{'} = \frac{m_{1} - m_{2}}{m_{1} + m_{2}} v_{2} + \frac{2 m_{2}}{m_{1} + m_{2}} v_{2} \\ and & v_{2}^{'} = \frac{m_{2} - m_{1}}{m_{1} + m_{2}} v_{2} + \frac{2 m_{1}}{m_{1} + m_{2}} v_{1} \end{aligned}$