Centre of Mass 3 Question 29
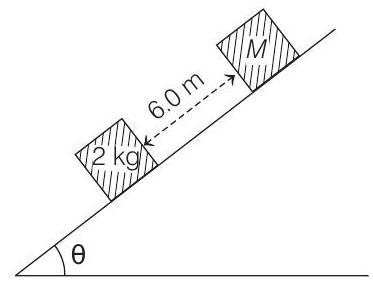
32. Two blocks of mass $2 kg$ and $M$ are at rest on an inclined plane and are separated by a distance of $6.0 m$ as shown. The coefficient of friction between each block and the inclined plane is 0.25 . The $2 kg$ block is given a velocity of $10.0 m / s$ up the inclined plane. It collides with $M$, comes back and has a velocity of $1.0 m / s$ when it reaches its initial position. The other block $M$ after the collision moves $0.5 m$ up and comes to rest. Calculate the coefficient of restitution between the blocks and the mass of the block $M$.
[Take $\sin \theta \approx \tan \theta=0.05$ and $g=10 m / s^{2}$ ]
$(1999,10 M)$
Show Answer
Answer:
Correct Answer: 32. $e=0.84, M=15.12 kg$
Solution:
- Let $v _1=$ velocity of block $2 kg$ just before collision,
$v _2=$ velocity of block $2 kg$ just after collision, and $v _3=$ velocity of block $M$ just after collision.
Applying work-energy theorem
(change in kinetic energy $=$ work done by all the forces) at different stages as shown in figure.
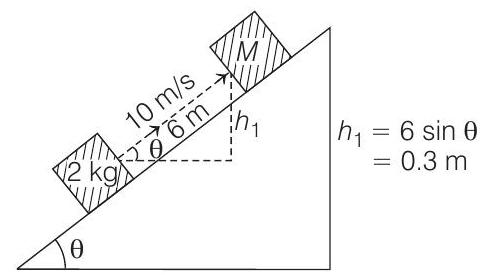
Figure 1.
$$ \begin{aligned} & \qquad \Delta KE=W _{\text {friction }}+W _{\text {gravity }} \\ & \\ & \begin{array}{l} \frac{1}{2} m{v _1^{2}-(10)^{2} }=-6 \mu m g \cos \theta-m g h _1 \\ \text { or } \\ \qquad v _1^{2}-100=-2\left[6 \mu g \cos \theta+g h _1\right] \\ \cos \theta=\sqrt{1-\sin ^{2} \theta}=\sqrt{1-(0.05)^{2}} \approx 0.99 \\ \Rightarrow \quad v _1^{2}=100-2[(6)(0.25)(10)(0.99)+(10)(0.3)] \\ \Rightarrow \quad v _1 \approx 8 m / s \end{array} \end{aligned} $$
Figure 2. $\Delta KE=W _{\text {friction }}+W _{\text {gravity }}$
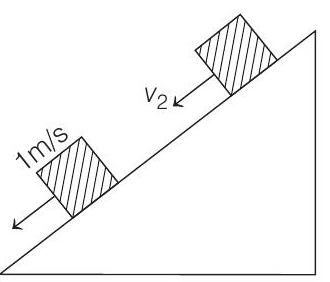
$$ \frac{1}{2} m\left[(1)^{2}-\left(v _2^{2}\right)\right]=-6 \mu m g \cos \theta+m g h _1 $$
or
$$ \begin{aligned} 1-v _2^{2} & =2\left[-6 \mu g \cos \theta+g h _1\right] \\ & =2[-(6)(0.25)(10)(0.99)+(10)(0.3)] \\ & =-23.7 \end{aligned} $$
$$ \therefore \quad v _2^{2}=24.7 $$
or $\quad v _2 \approx 5 m / s$
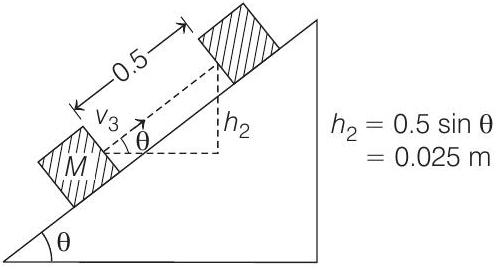
Figure 3. $\triangle KE=W _{\text {friction }}+W _{\text {gravity }}$
$$ \frac{1}{2} M\left[0-v _3^{2}\right]=-(0.5)(\mu)(M) g \cos \theta-M g h _2 $$
 or
or
or $\quad v _3^{2}=(0.25)(10)(0.99)+2(10)(0.025)$
or $\quad v _3^{2}=2.975 \quad \Rightarrow \quad \therefore \quad v _3 \approx 1.72 m / s$
Now,
(a) Coefficient of restitution
$$ \begin{aligned} & =\frac{\text { Relative velocity of separation }}{\text { Relative velocity of approach }} \\ & =\frac{v _2+v _3}{v _1}=\frac{5+1.72}{8}=\frac{6.72}{8} \text { or } e \approx 0.84 \end{aligned} $$
(b) Applying conservation of linear momentum before and after collision
$$ \begin{aligned} 2 v _1 & =M v _3-2 v _2 \\ \therefore \quad M & =\frac{2\left(v _1+v _2\right)}{v _3} \\ & =\frac{2(8+5)}{1.72}=\frac{26}{1.72} \\ M & \approx 15.12 kg \end{aligned} $$






