Centre of Mass 3 Question 27
30. A particle of mass $4 m$ which is at rest explodes into three fragments. Two of the fragments each of mass $m$ are found to move with a speed $v$ each in mutually perpendicular directions. The total energy released in the process of explosion is
$(1987,2 M)$
Integer Answer Type Questions
Show Answer
Solution:
- From conservation of linear momentum $p _3$ should be $\sqrt{2} m v$ in a direction opposite to $\mathbf{p} _{12}$ (resultant of $\mathbf{p} _1$ and $\mathbf{p} _2$ ). Let $v^{\prime}$ be the speed of third fragment, then
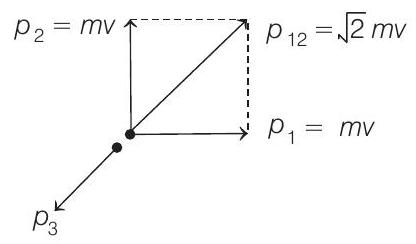
$$ \begin{aligned} (2 m) v^{\prime} & =\sqrt{2} m v \\ \therefore \quad v^{\prime} & =\frac{v}{\sqrt{2}} \end{aligned} $$
$\therefore$ Total energy released is,
$$ \begin{aligned} E & =2 \frac{1}{2} m v^{2}+\frac{1}{2}(2 m) v^{\prime 2} \\ & =m v^{2}+m \frac{v}{\sqrt{2}}^{2}=\frac{3}{2} m v^{2} \end{aligned} $$






