Centre of Mass 2 Question 6
7. Two blocks $A$ and $B$ each of mass $m$, are connected by a massless spring of natural length $L$ and spring constant $k$. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown in figure. A third identical block $C$, also of mass $m$, moves on the floor with a speed $v$ along the line joining $A$ and $B$, and collides elastically with $A$. Then
(1993, 2M)
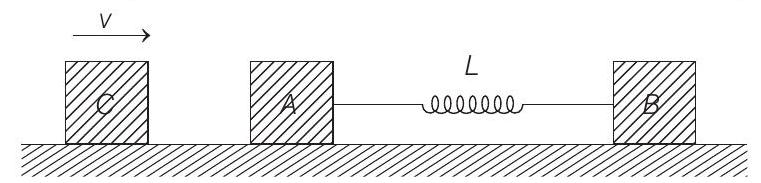
(a) the kinetic energy of the $A-B$ system, at maximum compression of the spring, is zero
(b) the kinetic energy of the $A-B$ system, at maximum compression of the spring, is $m v^{2} / 4$
(c) the maximum compression of the spring is $v \sqrt{(m / k)}$
(d) the maximum compression of the spring is $v \sqrt{\frac{m}{2 k}}$
Analytical & Descriptive Questions
Show Answer
Answer:
Correct Answer: 7. (b, d)
Solution:
- After collision between $C$ and $A, C$ stops while $A$ moves with speed of $C$ i.e. $v$ [in head on elastic collision, two equal masses exchange their velocities]. At maximum compression, $A$ and $B$ will move with same speed $v / 2$ (From conservation of linear momentum).
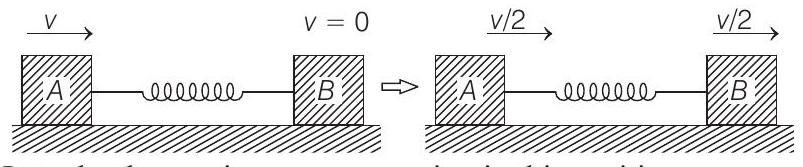
Let $x$ be the maximum compression in this position.
$\therefore KE$ of $A-B$ system at maximum compression
$$ =\frac{1}{2}(2 m) \frac{v}{2}^{2} \text { or } K _{\max }=m v^{2} / 4 $$
From conservation of mechanical energy in two positions shown in above figure
$$ \text { or } \quad \begin{aligned} \frac{1}{2} m v^{2} & =\frac{1}{4} m v^{2}+\frac{1}{2} k x^{2} \\ \frac{1}{2} k x^{2} & =\frac{1}{4} m v^{2} \\ \Rightarrow \quad x & =v \sqrt{\frac{m}{2 k}} \text { (Maximum compression) } \end{aligned} $$
