Centre of Mass 1 Question 8
8. Look at the drawing given in the figure, which has been drawn with ink of uniform line-thickness. The mass of ink used to draw each of the two inner circles, and each of the two line segments is $m$. The mass of the ink used to draw the outer circle is $6 m$.
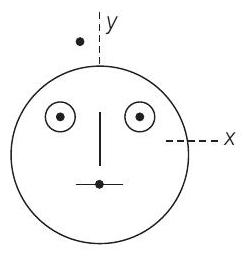The coordinates of the centres of the different parts are : outer circle $(0,0)$, left inner circle $(-a, a)$, right inner circle $(a, a)$, vertical line $(0,0)$ and horizontal line $(0,-a)$. The $y$-coordinate of the centre of mass of the ink in this drawing is
(2009)
(a) $\frac{a}{10}$
(b) $\frac{a}{8}$
(c) $\frac{a}{12}$
(d) $\frac{a}{3}$
Show Answer
Answer:
Correct Answer: 8. (a)
Solution:
- $y _{CM}=\frac{m _1 y _1+m _2 y _2+m _3 y _3+m _4 y _4+m _5 y _5}{m _1+m _2+m _3+m _4+m _5}$
$$ =\frac{(6 m)(0)+(m)(a)+m(a)+m(0)+m(-a)}{6 m+m+m+m+m}=\frac{a}{10} $$
