Centre of Mass 1 Question 6
6. Consider regular polygons with number of sides
(2017 Adv.)
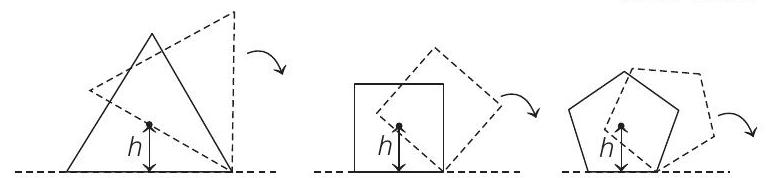
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 6. (d)
Solution:






