Centre of Mass 1 Question 5
5. An
(2019 Main, 9 Jan)
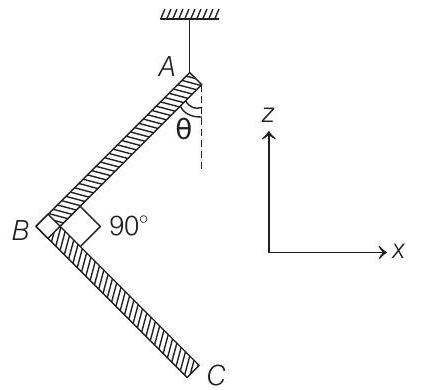
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 5. (d)
Solution:
- Key Idea The centre of mass of a thin rod of uniform density lies at its centre.
The given system of rods can be drawn using geometry as,
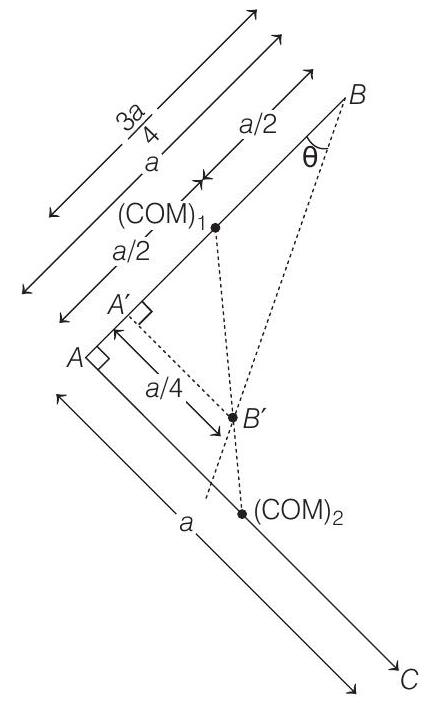
where,
So, in






