Centre of Mass 1 Question 4
4. The position vector of the centre of mass $\mathbf{r} _{cm}$ of an asymmetric uniform bar of negligible area of cross-section as shown in figure is
(2019 Main, 12 Jan I)
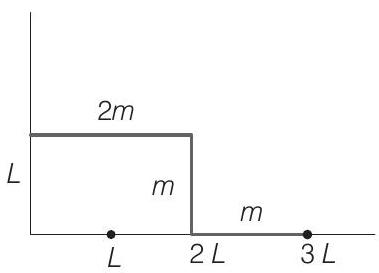
(a) $\mathbf{r}=\frac{13}{8} L \hat{\mathbf{x}}+\frac{5}{8} L \hat{\mathbf{y}}$
(b) $\mathbf{r}=\frac{11}{8} L \hat{\mathbf{x}}+\frac{3}{8} L \hat{\mathbf{y}}$
(c) $\mathbf{r}=\frac{3}{8} L \hat{\mathbf{x}}+\frac{11}{8} L \hat{\mathbf{y}}$
(d) $\mathbf{r}=\frac{5}{8} L \hat{\mathbf{x}}+\frac{13}{8} L \hat{\mathbf{y}}$
Show Answer
Answer:
Correct Answer: 4. (a)
Solution:
- Coordinates of centre of mass (COM) are given by
and
$$ \begin{aligned} X _{COM} & =\frac{m _1 x _1+m _2 x _2+m _3 x _3}{m _1+m _2+m _3} \\ Y _{COM} & =\frac{m _1 y _1+m _2 y _2+m _3 y _3}{m _1+m _2+m _3} \end{aligned} $$
For given system of rods, masses and coordinates of centre of rods are as shown.
So, $X _{COM}=\frac{2 m L+m 2 L+m \frac{5 L}{2}}{4 m}=\frac{13}{8} L$
and $Y _{COM}=\frac{2 m L+m \times \frac{L}{2}+m \times 0}{4 m}=\frac{5 L}{8}$
So, position vector of $COM$ is
$$ \begin{aligned} r _{com} & =X _{COM} \hat{\mathbf{x}}+Y _{COM} \hat{\mathbf{y}} \\ & =\frac{13}{8} L \hat{\mathbf{x}}+\frac{5}{8} L \hat{\mathbf{y}} \end{aligned} $$
