Centre of Mass 1 Question 3
3. Four particles
(2019 Main, 8 April I)
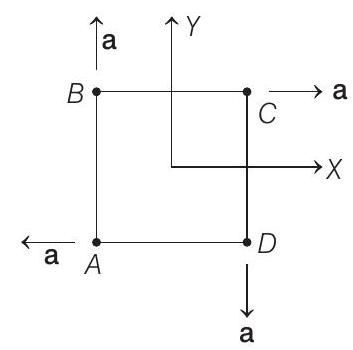
(a)
(b)
(c) zero
(d)
Show Answer
Answer:
Correct Answer: 3. (a)
Solution:
- For a system of discrete masses, acceleration of centre of mass (CM) is given by
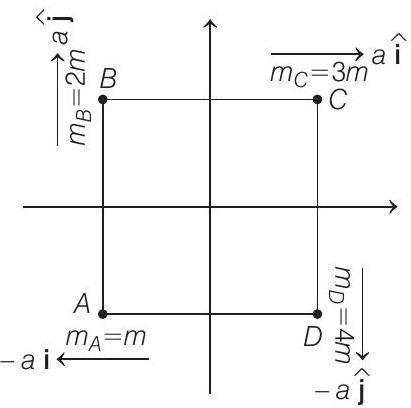
where,






