Centre of Mass 1 Question 14
14. A small sphere of radius
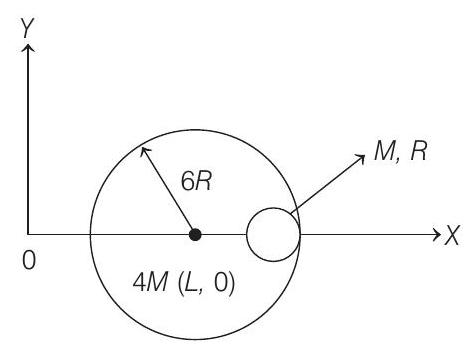
friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the larger sphere when the smaller sphere reaches the other extreme position.
(1996, 3 M)
Show Answer
Answer:
Correct Answer: 14.
Solution:
- Since, all the surfaces are smooth, no external force is acting on the system in horizontal direction. Therefore, the centre of mass of the system in horizontal direction remains stationary.
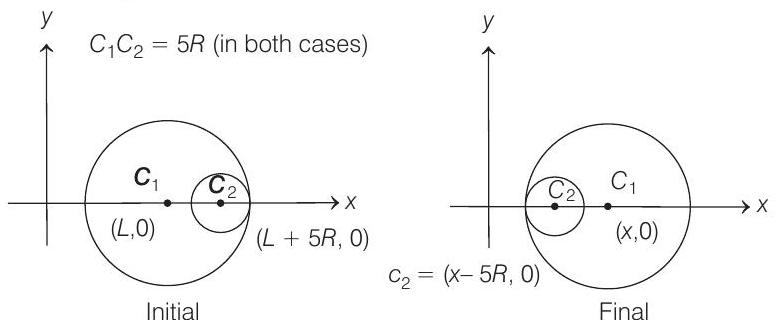
Let
Equating Eqs. (i) and (ii), we have
Therefore, coordinates of large sphere, when the smaller sphere reaches the other extreme position, are






