SATHEE: Centre of Mass 1 Question 12

Centre of Mass 1 Question 12

12. A block of mass $M$ has a circular cut with a frictionless surface as shown. The block rests on the horizontal frictionless surfaced of a fixed table. Initially the right edge of the block is at $x = 0$ , in a coordinate system fixed to the table. A point mass $m$ is released from rest at the topmost point of the path as shown and it slides down. When the mass loses contact with the block, its position is $x$ and the velocity is $v$ . At that instant, which of the following option is/are correct?

(2017 Adv.)

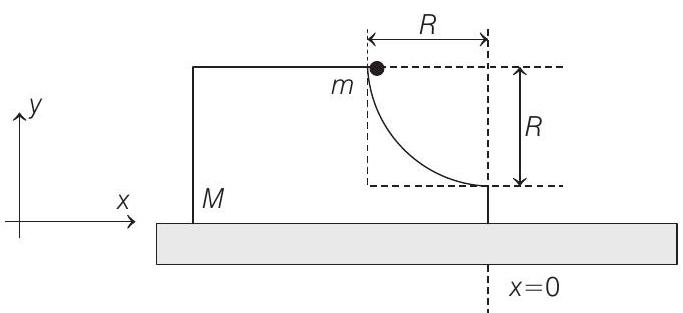
(a) The velocity of the point mass $m$ is $v = \sqrt{\frac{2 g R}{1 + \frac{m}{M}}}$

(b) The $x$ component of displacement of the centre of mass of the block $M$ is $- \frac{m R}{M + m}$

(d) The velocity of the block $M$ is $V = - \frac{m}{M} \sqrt{2 g R}$

True/False

Show Answer

Answer:

Correct Answer: 12. (a)

Solution:

$Δ x_{c m}$ of the block and point mass system $= 0$

$∴ m (x + R) + M x = 0$

where, $x$ is displacement of the block.

Solving this equation, we get

$x = - \frac{m R}{M + m}$

From conservation of momentum and mechanical energy of the combined system

$0 = m v - M V \Rightarrow m g R = \frac{1}{2} m v^{2} + \frac{1}{2} M V^{2}$

Solving these two equations, we get

$∴ v = \sqrt{\frac{2 g R}{1 + \frac{m}{M}}}$

पिछला

अगला

Centre of Mass 1 Question 12

True/False

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Centre of Mass 1 Question 12

True/False

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu