Vectors 5 Question 9
9. Incident ray is along the unit vector $\hat{\mathbf{v}}$ and the reflected ray is along the unit vector $\hat{\mathbf{w}}$. The normal is along unit vector $\hat{\mathbf{a}}$ outwards. Express $\hat{\mathbf{w}}$ in terms of $\hat{\mathbf{a}}$ and $\hat{\mathbf{v}}$.
$(2005,4$ M)
Show Answer
Answer:
Correct Answer: 9. $-\hat{\mathbf{i}}+3 \hat{\mathbf{j}}+3 \hat{\mathbf{k}}$ and $3 \hat{\mathbf{i}}-\hat{\mathbf{j}}-\hat{\mathbf{k}}$
Solution:
- Since, $\hat{\mathbf{v}}$ is unit vector along the incident ray and $\hat{\mathbf{w}}$ is the unit vector along the reflected ray.
Hence, $\hat{\mathbf{a}}$ is a unit vector along the external bisector of $\hat{\mathbf{v}}$ and $\hat{\mathbf{w}}$.
$\therefore \hat{\mathbf{w}}-\hat{\mathbf{v}}=\lambda \hat{\mathbf{a}}$
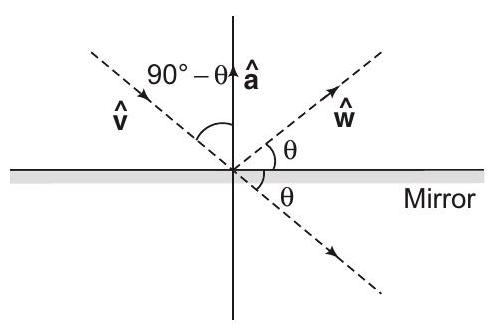
On squaring both sides, we get
$$ \begin{aligned} & \Rightarrow 1+1-\hat{\mathbf{w}} \cdot \hat{\mathbf{v}}=\lambda^{2} \Rightarrow 2-2 \cos 2 \theta=\lambda^{2} \\ & \Rightarrow \quad \lambda=2 \sin \theta \end{aligned} $$
where, $2 \theta$ is the angle between $\hat{\mathbf{v}}$ and $\hat{\mathbf{w}}$.
Hence, $\hat{\mathbf{w}}-\hat{\mathbf{v}}=2 \sin \theta \cdot \hat{\mathbf{a}}=2 \cos \left(90^{\circ}-\theta\right) \hat{\mathbf{a}}=-(2 \hat{\mathbf{a}} \cdot \hat{\mathbf{v}}) \hat{\mathbf{a}}$
$\Rightarrow \quad \hat{\mathbf{w}}=\hat{\mathbf{v}}-2(\hat{\mathbf{a}} \cdot \hat{\mathbf{v}}) \hat{\mathbf{a}}$
