Vectors 5 Question 12
12. Prove, by vector methods or otherwise, that the point of intersection of the diagonals of a trapezium lies on the line passing through the mid-points of the parallel sides. (you may assume that the trapezium is not a parallelogram).
(1998, 8M)
Show Answer
Solution:
- Let
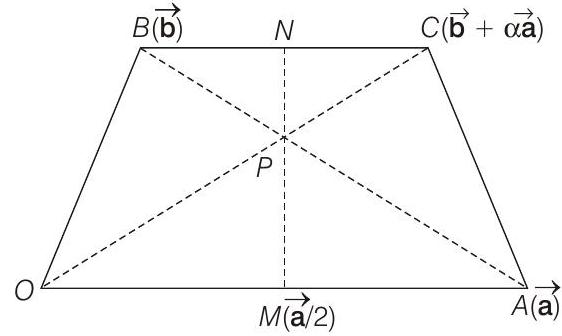
Since,
Equation of
equation of
Let
Since,
Thus, position vector of
Equation of
For






