Vectors 4 Question 11
11. Consider the cube in the first octant with sides
Show Answer
Answer:
Correct Answer: 11. (0.5)
Solution:
- (0.5) Here,
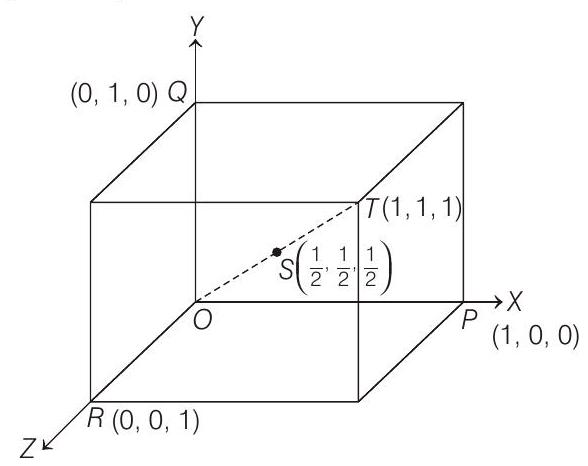
Now,
and
and
Now,






