Vectors 3 Question 3
3. If $\overrightarrow{\mathbf{a}}, \overrightarrow{\mathbf{b}}, \overrightarrow{\mathbf{c}}$ and $\overrightarrow{\mathbf{d}}$ are the unit vectors such that $(\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}) \cdot(\overrightarrow{\mathbf{c}} \times \overrightarrow{\mathbf{d}})=1$ and $\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{c}}=\frac{1}{2}$, then
(2009)
(a) $\overrightarrow{\mathbf{a}}, \overrightarrow{\mathbf{b}}, \overrightarrow{\mathbf{c}}$ are non-coplanar
(b) $\overrightarrow{\mathbf{a}}, \overrightarrow{\mathbf{b}}, \overrightarrow{\mathbf{d}}$ are non-coplanar
(c) $\overrightarrow{\mathbf{b}}, \overrightarrow{\mathbf{d}}$ are non-parallel
(d) $\overrightarrow{\mathbf{a}}, \overrightarrow{\mathbf{d}}$ are parallel and $\overrightarrow{\mathbf{b}}, \overrightarrow{\mathbf{c}}$ are parallel
Show Answer
Answer:
Correct Answer: 3. (c)
Solution:
- Let angle between $\overrightarrow{\mathbf{a}}$ and $\overrightarrow{\mathbf{b}}$ be $\theta _1, \overrightarrow{\mathbf{c}}$ and $\overrightarrow{\mathbf{d}}$ be $\theta _2$ and $\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}$ and $\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathbf{d}}$ be $\theta$.
Since, $\quad(\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}) \cdot(\overrightarrow{\mathbf{c}} \times \overrightarrow{\mathbf{d}})=1$
$\Rightarrow \quad \sin \theta _1 \cdot \sin \theta _2 \cdot \cos \theta=1$
$\Rightarrow \quad \theta _1=90^{\circ}, \theta _2=90^{\circ}, \theta=0^{\circ}$
$\Rightarrow \overrightarrow{\mathbf{a}} \perp \overrightarrow{\mathbf{b}}, \overrightarrow{\mathbf{c}} \perp \overrightarrow{\mathbf{d}},(\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}) |(\overrightarrow{\mathbf{c}} \times \overrightarrow{\mathbf{d}})$
So, $\quad \overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}=k(\overrightarrow{\mathbf{c}} \times \overrightarrow{\mathbf{d}})$ and $\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}=k(\overrightarrow{\mathbf{c}} \times \overrightarrow{\mathbf{d}})$
$\Rightarrow \quad(\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}) \cdot \overrightarrow{\mathbf{c}}=k(\overrightarrow{\mathbf{c}} \times \overrightarrow{\mathbf{d}}) \cdot \overrightarrow{\mathbf{c}}$
an $d(\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}) \cdot \overrightarrow{\mathbf{d}}=k(\overrightarrow{\mathbf{c}} \times \overrightarrow{\mathbf{d}}) \cdot \overrightarrow{\mathbf{d}}$
$\Rightarrow \quad[\overrightarrow{\mathbf{a}} \overrightarrow{\mathbf{b}} \overrightarrow{\mathbf{c}}]=0 \quad$ and $\quad[\overrightarrow{\mathbf{a}} \overrightarrow{\mathbf{b}} \overrightarrow{\mathbf{d}}]=0$
$\Rightarrow \overrightarrow{\mathbf{a}}, \overrightarrow{\mathbf{b}}, \overrightarrow{\mathbf{c}}$ and $\overrightarrow{\mathbf{a}}, \overrightarrow{\mathbf{b}}, \overrightarrow{\mathbf{d}}$ are coplanar vectors, so options (a) and (b) are incorrect.
Let $\overrightarrow{\mathbf{b}} | \overrightarrow{\mathbf{d}} \Rightarrow \overrightarrow{\mathbf{b}}= \pm \overrightarrow{\mathbf{d}}$
$$ \begin{aligned} & \text { As } \quad(\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}) \cdot(\overrightarrow{\mathbf{c}} \times \overrightarrow{\mathbf{d}})=1 \Rightarrow(\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}) \cdot(\overrightarrow{\mathbf{c}} \times \overrightarrow{\mathbf{b}})= \pm 1 \\ & \Rightarrow \quad[\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}} \overrightarrow{\mathbf{c}} \overrightarrow{\mathbf{b}}]= \pm 1 \Rightarrow[\overrightarrow{\mathbf{c}} \overrightarrow{\mathbf{b}} \overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}]= \pm 1 \\ & \Rightarrow \overrightarrow{\mathbf{c}} \cdot[\overrightarrow{\mathbf{b}} \times(\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}})]= \pm 1 \Rightarrow \overrightarrow{\mathbf{c}} \cdot[\overrightarrow{\mathbf{a}}-(\overrightarrow{\mathbf{b}} \cdot \overrightarrow{\mathbf{a}}) \overrightarrow{\mathbf{b}}]= \pm 1 \\ & \Rightarrow \quad \overrightarrow{\mathbf{c}} \cdot \overrightarrow{\mathbf{a}}= \pm 1 \quad[\because \overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}}=0] \end{aligned} $$
which is a contradiction, so option (c) is correct.
Let option (d) is correct.
$$ \begin{aligned} \Rightarrow & \overrightarrow{\mathbf{d}}= \pm \overrightarrow{\mathbf{a}} \\ \text { and } & \overrightarrow{\mathbf{c}}= \pm \overrightarrow{\mathbf{b}} \\ \text { As } & (\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}) \cdot(\overrightarrow{\mathbf{c}} \times \overrightarrow{\mathbf{d}})=1 \\ \Rightarrow & (\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}) \cdot(\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathbf{a}})= \pm 1 \end{aligned} $$
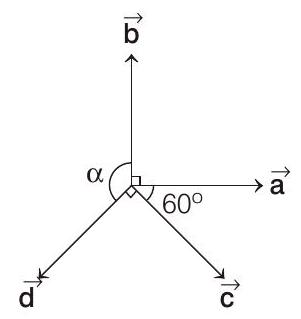
which is a contradiction, so option (d) is incorrect. Alternatively, options (c) and (d) may be observed from the given figure.
