Vectors 2 Question 14
14. Let the vectors
Statement I
because
Statement II
(2007, 3M)
Show Answer
Answer:
Correct Answer: 14. (c)
Solution:
- Since,
But for Statement II, we have
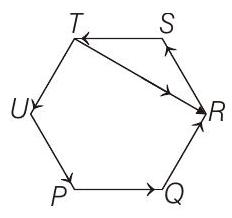
which is not possible as
Hence, Statement I is true and Statement II is false.






