Vectors 1 Question 7
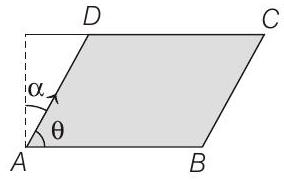
8. Two adjacent sides of a parallelogram $A B C D$ are given by $\overrightarrow{A B}=2 \hat{i}+10 \hat{j}+11 \hat{k}$ and $\overrightarrow{A D}=-\hat{i}+2 \hat{j}+2 \hat{k}$. The side $A D$ is rotated by an acute angle $\alpha$ in the plane of the parallelogram so that $A D$ becomes $A D$ ‘. If $A D$ ’ makes a right angle with the side $A B$, then the cosine of the angle $\alpha$ is given by
(2010)
(a) $\frac{8}{9}$
(b) $\frac{\sqrt{17}}{9}$
(c) $\frac{1}{9}$
(d) $\frac{4 \sqrt{5}}{9}$
Show Answer
Answer:
Correct Answer: 8. (b)
Solution:
- $\overrightarrow{\mathbf{A B}}=2 \hat{\mathbf{i}}+10 \hat{\mathbf{j}}+11 \hat{\mathbf{k}}, \quad \overrightarrow{\mathbf{A D}}=-\hat{\mathbf{i}}+2 \hat{\mathbf{j}}+2 \hat{\mathbf{k}}$
Angle ’ $\theta$ ’ between $\overrightarrow{\mathbf{A B}}$ and $\overrightarrow{\mathbf{A D}}$ is
$$ \begin{aligned} & \cos (\theta)=\left|\frac{\overrightarrow{\mathbf{A B}} \cdot \overrightarrow{\mathbf{A D}}}{|\overrightarrow{\mathbf{A B}}||\overrightarrow{\mathbf{A D}}|}\right|=\left|\frac{-2+20+22}{(15)(3)}\right|=\frac{8}{9} \\ & \Rightarrow \quad \sin (\theta)=\frac{\sqrt{17}}{9} \end{aligned} $$
Since, $\quad \alpha+\theta=90^{\circ}$
$\therefore \quad \cos (\alpha)=\cos \left(90^{\circ}-\theta\right)=\sin (\theta)=\frac{\sqrt{17}}{9}$
