Vectors 1 Question 25
26. Show, by vector methods, that the angular bisectors of a triangle are concurrent and find an expression for the position vector of the point of concurrency in terms of the position vectors of the vertices.
(2001, 5M)
Show Answer
Answer:
Correct Answer: 26. (b)
Solution:
- Let $A D$ be the angular bisector of angle $A$. Let $B C, A C$ and $A B$ are $\alpha, \beta$ and $\gamma$, respectively. Then, $\frac{B D}{D C}=\frac{\gamma}{\beta}$.
Hence, position vector of $D=\frac{\gamma \overrightarrow{\mathbf{c}}+\beta \overrightarrow{\mathbf{b}}}{\gamma+\beta}$. On $A D$, there lies a point $I$ which divides it in ratio $\gamma+\beta: \alpha$.
Now, position vector of $I=\frac{\alpha \overrightarrow{\mathbf{a}}+\beta \overrightarrow{\mathbf{b}}+\gamma \overrightarrow{\mathbf{c}}}{\alpha+\beta+\gamma}$
which is symmetric in $\overrightarrow{\mathbf{a}}, \overrightarrow{\mathbf{b}}, \overrightarrow{\mathbf{c}}, \alpha, \beta$ and $\gamma$.
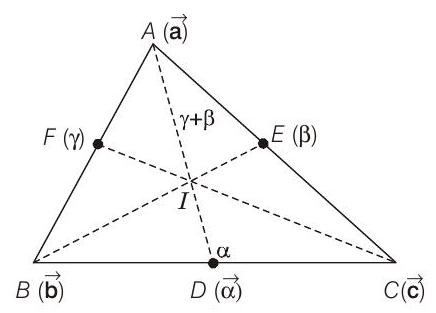
Hence $I$ lies on every angle bisector and angle bisectors are concurrent.
Here, $\alpha=|\overrightarrow{\mathbf{b}}-\overrightarrow{\mathbf{c}}|, \beta=|\overrightarrow{\mathbf{a}}-\overrightarrow{\mathbf{c}}|, \gamma=|\overrightarrow{\mathbf{a}}-\overrightarrow{\mathbf{b}}|$.
