Vectors 1 Question 21
22. $A, B, C$ and $D$, are four points in a plane with position vectors $\overrightarrow{\mathbf{a}}, \overrightarrow{\mathbf{b}}, \overrightarrow{\mathbf{c}}$ and $\overrightarrow{\mathbf{d}}$ respectively such that
$$ (\overrightarrow{\mathbf{a}}-\overrightarrow{\mathbf{d}}) \cdot(\overrightarrow{\mathbf{b}}-\overrightarrow{\mathbf{c}})=(\overrightarrow{\mathbf{b}}-\overrightarrow{\mathbf{d}}) \cdot(\overrightarrow{\mathbf{c}}-\overrightarrow{\mathbf{a}})=0 $$
The point $D$, then, is the… of the $\triangle A B C . \quad(1984,2 M)$
Show Answer
Answer:
Correct Answer: 22. (b)
Solution:
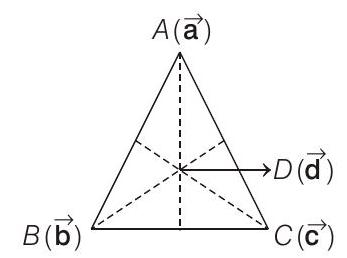
- As, $(\overrightarrow{\mathbf{a}}-\overrightarrow{\mathbf{d}}) \cdot(\overrightarrow{\mathbf{b}}-\overrightarrow{\mathbf{c}})=(\overrightarrow{\mathbf{b}}-\overrightarrow{\mathbf{d}}) \cdot(\overrightarrow{\mathbf{c}}-\overrightarrow{\mathbf{a}})=0$
$$ \Rightarrow \quad A D \perp B C \quad \text { and } \quad B D \perp C A $$
which clearly represents from figure that $D$ is orthocentre of $\triangle A B C$.
