Trigonometrical Equations 2 Question 3
3. Let
(2012)
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 3.
Solution:
- PLAN It is based on range of
Description of Situation As
Also,
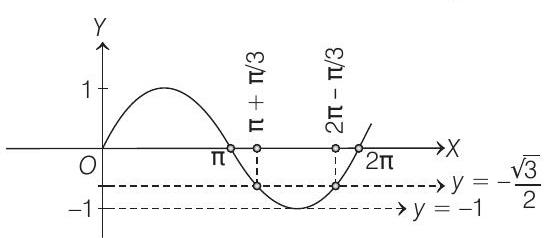
Here,
From Eq. (i),
or
or






