Trigonometrical Equations 2 Question 2
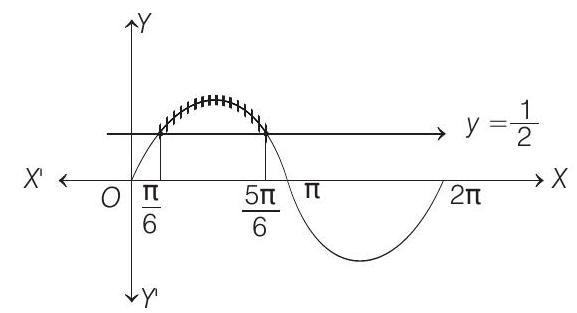
2. The set of values of $\theta$ satisfying the inequation $2 \sin ^{2} \theta-5 \sin \theta+2>0$, where $0<\theta<2 \pi$, is
(2006, 3M)
(a) $0, \frac{\pi}{6} \cup \frac{5 \pi}{6}, 2 \pi$
(b) $0, \frac{\pi}{6} \cup \frac{5 \pi}{6}, 2 \pi$
(c) $0, \frac{\pi}{3} \cup \frac{2 \pi}{3}, 2 \pi$
(d) None of the above
Show Answer
Answer:
Correct Answer: 2. (a)
Solution:
- Since, $2 \sin ^{2} \theta-5 \sin \theta+2>0$
$\Rightarrow \quad(2 \sin \theta-1)(\sin \theta-2)>0$
[where, $(\sin \theta-2)<0, \forall \theta \in R$ ]
$$ \therefore \quad(2 \sin \theta-1)<0 $$
$\Rightarrow \quad \sin \theta<\frac{1}{2}$
$\therefore$ From the graph, $\theta \in 0, \frac{\pi}{6} \cup \frac{5 \pi}{6}, 2 \pi$
