Theory of Equations 5 Question 9
9. Let
(a)
(b)
(c)
(d)
Show Answer
Solution:
- Given,
Also,
or
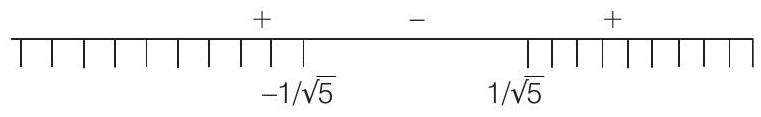
Also,
From Eqs. (i) and (ii), we get






