Theory of Equations 4 Question 9
10. Let
Show Answer
Solution:
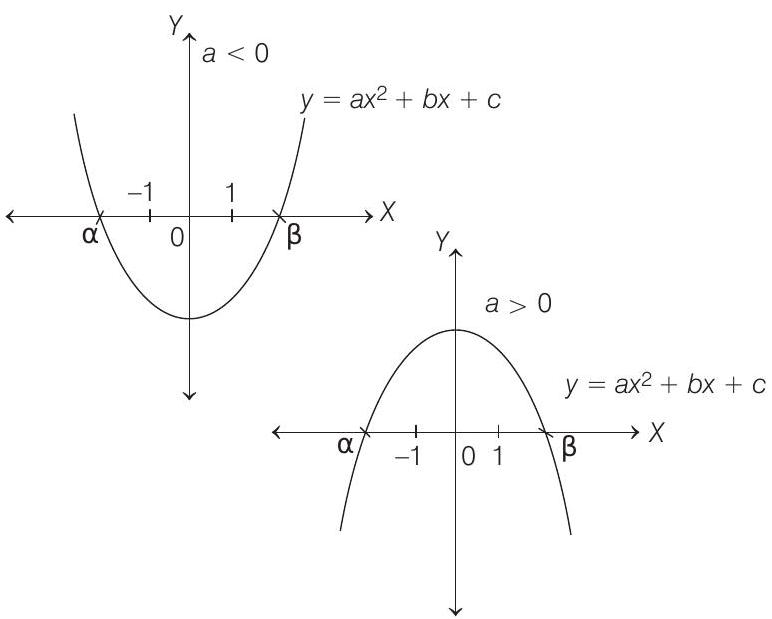
From figure, it is clear that, if
On dividing by
On combining both, we get






