Theory of Equations 4 Question 3
3. If both the roots of the quadratic equation $x^{2}-m x+4=0$ are real and distinct and they lie in the interval $[1,5]$ then $m$ lies in the interval
(2019 Main, 9 Jan II)
(a) $(4,5)$
(b) $(-5,-4)$
(c) $(5,6)$
(d) $(3,4)$
Show Answer
Solution:
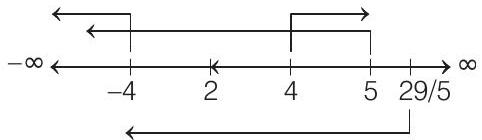
- According to given information, we have the following graph
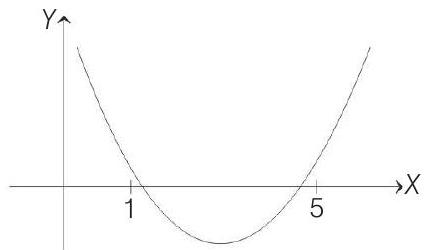
Now, the following conditions should satisfy
(i) $D>0 \Rightarrow b^{2}-4 a c>0$
$$ \begin{array}{lc} \Rightarrow & m^{2}-4 \times 1 \times 4>0 \\ \Rightarrow & m^{2}-16>0 \\ \Rightarrow & (m-4)(m+4)>0 \\ \Rightarrow & m \in(-\infty,-4) \cup(4, \infty) \end{array} $$
(ii) The vertex of the parabola should lie between $x=1$ and $x=5$
$$ \therefore \quad-\frac{b}{2 a} \in(1,5) \Rightarrow 1<\frac{m}{2}<5 \Rightarrow m \in(2,10) $$
(iii) $f(1)>0 \Rightarrow 1-m+4>0$
$$ \Rightarrow m<5 \Rightarrow m \in(-\infty, 5) $$
(iv) $f(5)>0 \Rightarrow 25-5 m+4>0 \Rightarrow 5 m<29 \Rightarrow m \in-\infty, \frac{29}{5}$
From the values of $m$ obtained in (i), (ii), (iii) and (iv), we get $m \in(4,5)$.
