Straight Line and Pair of Straight Lines 3 Question 3
4. Area of the parallelogram formed by the lines
(a)
(b)
(c)
(d)
(2001, 1M)
Show Answer
Answer:
Correct Answer: 4. (d)
Solution:
- Let lines
The point of intersection
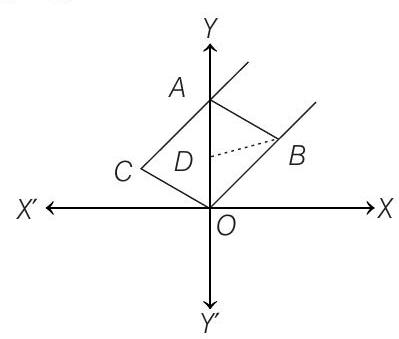
Now, area of a parallelogram
depending upon whether






