Straight Line and Pair of Straight Lines 3 Question 2
3. Two sides of a rhombus are along the lines,
(2016 Main)
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 3. (c)
Solution:
- As the given lines
On solving
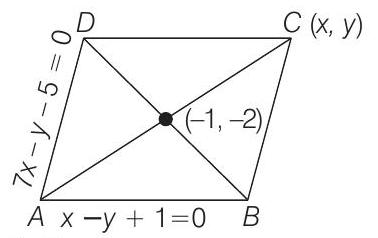
Let the coordinate of point
Hence, coordinates of
Note that, vertices
Since, option (c) satisfies






