Straight Line and Pair of Straight Lines 3 Question 1
1. A triangle has a vertex at $(1,2)$ and the mid-points of the two sides through it are $(-1,1)$ and $(2,3)$. Then, the centroid of this triangle is
(2019 Main, 12 April II)
(a) $1, \frac{7}{3}$
(b) $\frac{1}{3}, 2$
(c) $\frac{1}{3}, 1$
(d) $\frac{1}{3}, \frac{5}{3}$
Show Answer
Answer:
Correct Answer: 1. (b)
Solution:
- Let a $\triangle A B C$ is such that vertices
$A(1,2), B\left(x _1 y _1\right)$ and $C\left(x _2, y _2\right)$.
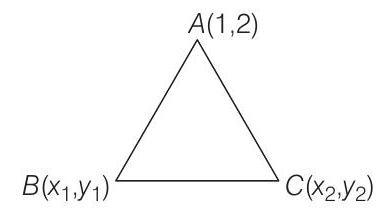
It is given that mid-point of side $A B$ is $(-1,1)$.
$$ \begin{array}{lc} \text { So, } & \frac{x _1+1}{2}=-1 \\ \text { and } & \frac{y _1+2}{2}=1 \\ \Rightarrow & x _1=-3 \text { and } y _1=0 \end{array} $$
So, point $B$ is $(-3,0)$
Also, it is given that mid-point of side $A C$ is $(2,3)$, so
$$ \begin{aligned} & & \frac{x _2+1}{2} & =2 \text { and } \frac{y _2+2}{2}=3 \\ \Rightarrow & & x _2 & =3 \text { and } y _2=4 \end{aligned} $$
So, point $C$ is $(3,4)$.
Now, centroid of $\triangle A B C$ is
$$ G \frac{1+(-3)+3}{3}, \frac{2+0+4}{3}=G \quad \frac{1}{3}, 2 $$
2 Given, $p x+q y+r=0$ is the equation of line such that $3 p+2 q+4 r=0$
$\begin{array}{rlrl}\text { Consider, } & 3 p+2 q+4 r & =0 \ \Rightarrow & \underline{3 p}+\underline{2 q}+r=0\end{array}$
$\Rightarrow \quad \frac{3 p}{4}+\frac{2 q}{4}+r=0$
$\Rightarrow \quad p \frac{3}{4}+q \frac{1}{2}+r=0$
$\Rightarrow \frac{3}{4}, \frac{1}{2}$ satisfy $p x+q y+r=0$
So, the lines always passes through the point $\frac{3}{4}, \frac{1}{2}$.
