Straight Line and Pair of Straight Lines 1 Question 69
69. One side of a rectangle lies along the line
Integer Answer Type Question
Show Answer
Answer:
Correct Answer: 69. 6 sq units
Solution:
- Since, the side
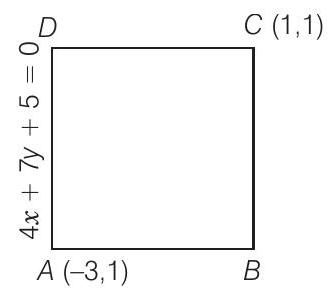
Since, it passes through
Now,
Since, it passes through
Now, equation of






