Straight Line and Pair of Straight Lines 1 Question 61
61. The equations of the perpendicular bisectors of the sides
(1986, 5M)
Show Answer
Solution:
- Let the coordinates of
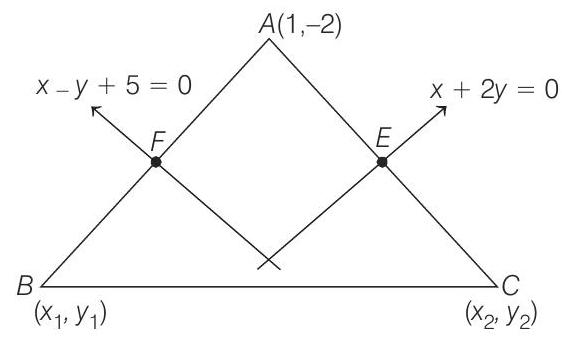
and
Let
Now,
Since,
On solving Eqs. (i) and (ii), we get
So, the coordinates of
Now,
Since,
On solving Eqs. (iii) and (iv), we get
So, the coordinates of
Thus, the equation of






