Straight Line and Pair of Straight Lines 1 Question 6
6. Slope of a line passing through
(2019 Main, 9 April I)
(a)
(b)
(c)
(d)
Show Answer
Solution:
- Let the slope of line is
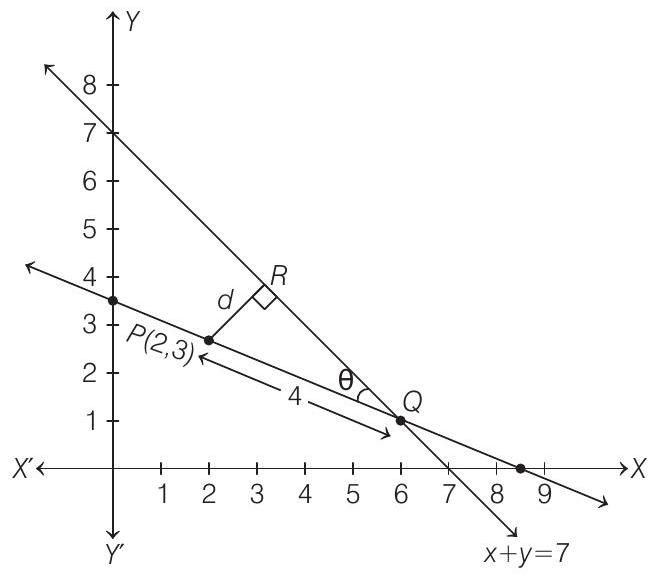
Since, the distance of a point
Now, in






