Straight Line and Pair of Straight Lines 1 Question 58
58. Straight lines $3 x+4 y=5$ and $4 x-3 y=15$ intersect at the point $A$. Points $B$ and $C$ are chosen on these two lines such that $A B=A C$. Determine the possible equations of the line $B C$ passing through the point $(1,2)$.
$(1990,4$ M)
Show Answer
Solution:
- Let $m _1$ and $m _2$ be the slopes of the lines $3 x+4 y=5$ and $4 x-3 y=15$, respectively.
Then, $m _1=-\frac{3}{4}$ and $m _2=\frac{4}{3}$
Clearly, $m _1 m _2=-1$. So, lines $A B$ and $A C$ are at right angle. Thus, the $\triangle A B C$ is a right angled isosceles triangle.
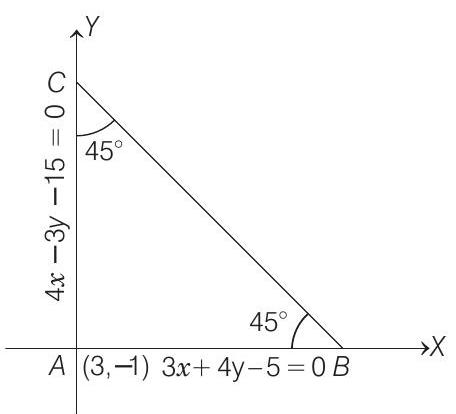
Hence, the line $B C$ through $(1,2)$ will make an angle of $45^{\circ}$ with the given lines. So, the possible equations of $B C$ are
$$ (y-2)=\frac{m \pm \tan 45^{\circ}}{1 \mp m \tan 45^{\circ}}(x-1) $$
where, $m=$ slope of $A B=-\frac{3}{4}$
$$ \begin{aligned} & \Rightarrow \quad(y-2)=\frac{-\frac{3}{4} \pm 1}{1 \mp-\frac{3}{4}}(x-1) \\ & \Rightarrow \quad(y-2)=\frac{-3 \pm 4}{4 \pm 3}(x-1) \\ & \Rightarrow \quad(y-2)=\frac{1}{7}(x-1) \\ & \text { and } \quad(y-2)=-7(x-1) \\ & \Rightarrow \quad x-7 y+13=0 \\ & \text { and } \quad 7 x+y-9=0 \end{aligned} $$
