Straight Line and Pair of Straight Lines 1 Question 56
56. Determine all values of $\alpha$ for which the point $\left(\alpha, \alpha^{2}\right)$ lies inside the triangles formed by the lines $2 x+3 y-1=0$,
$$ x+2 y-3=0,5 x-6 y-1=0 $$
(1992, 6M)
Show Answer
Solution:
- Given lines are $2 x+3 y-1=0$
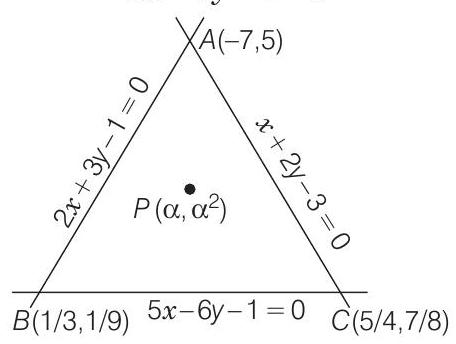
On solving Eqs. (i), (ii) and (iii), we get the vertices of a triangle are $A(-7,5), B \frac{1}{3}, \frac{1}{9}$ and $C \frac{5}{4}, \frac{7}{8}$.
Let $P\left(\alpha, \alpha^{2}\right)$ be a point inside the $\triangle A B C$. Since, $A$ and $P$ are on the same side of $5 x-6 y-1=0$, both $5(-7)-6(5)-1$ and $5 \alpha-6 \alpha^{2}-1$ must have the same sign, therefore
$$ \begin{array}{cc} & 5 \alpha-6 \alpha^{2}-1<0 \\ \Rightarrow & 6 \alpha^{2}-5 \alpha+1>0 \\ \Rightarrow & (3 \alpha-1)(2 \alpha-1)>0 \\ & \alpha<\frac{1}{3} \text { or } \alpha>\frac{1}{2} \end{array} $$
Also, since $P\left(\alpha, \alpha^{2}\right)$ and $C \frac{5}{4}, \frac{7}{8}$ lie on the same side of $2 x+3 y-1=0$, therefore both $2 \frac{5}{4}+3 \frac{7}{8}-1$ and $2 \alpha+3 \alpha^{2}-1$ must have the same sign.
Therefore,
$$ 2 \alpha+3 \alpha^{2}-1>0 $$
$$ \begin{array}{rlrl} \Rightarrow & (\alpha+1) & \alpha-\frac{1}{3}>0 \\ \Rightarrow & \alpha<-1 \cup \alpha>1 / 3 \end{array} $$
and lastly $\frac{1}{3}, \frac{1}{9}$ and $P\left(\alpha, \alpha^{2}\right)$ lie on the same side of the line therefore, $\frac{1}{3}+2 \frac{1}{9}-3$ and $\alpha+2 \alpha^{2}-3$ must have the same sign. Therefore, $2 \alpha^{2}+\alpha-3<0$
$$ \begin{array}{ll} \Rightarrow & 2 \alpha(\alpha-1)+3(\alpha-1)<0 \\ \Rightarrow & (2 \alpha+3)(\alpha-1)<0 \Rightarrow-\frac{2}{3}<\alpha<1 \end{array} $$
On solving Eqs. (i), (ii) and (iii), we get the common answer is $-\frac{3}{2}<\alpha<-1 \cup \frac{1}{2}<\alpha<1$.
