Straight Line and Pair of Straight Lines 1 Question 54
54. A rectangle $P Q R S$ has its side $P Q$ parallel to the line $y=m x$ and vertices $P Q$ and $S$ on the lines $y=a, x=b$ and $x=-b$, respectively. Find the locus of the vertex $R$.
$(1996,2 M)$
Show Answer
Solution:
- Let the coordinates of $Q$ be $(b, \alpha)$ and that of $S$ be $(-b, \beta)$. Suppose, $P R$ and $S Q$ meet in $G$. Since, $G$ is mid point of $S Q$, its $x$-coordinate must be 0 . Let the coordinates of $R$ be $(h, k)$.
Since, $G$ is mid point of $P R$, the $x$-coordinate of $P$ must be $-h$ and as $P$ lies on the line $y=a$, the coordinates of $P$ are $(-h, a)$. Since, $P Q$ is parallel to $y=m x$, slope of $P Q=m$
$$ \Rightarrow \quad \frac{\alpha-a}{b+h}=m $$
Again,
$$ \text { Slope of } R Q=-\frac{1}{m} \Rightarrow \frac{k-\alpha}{h-b}=-\frac{1}{m} $$
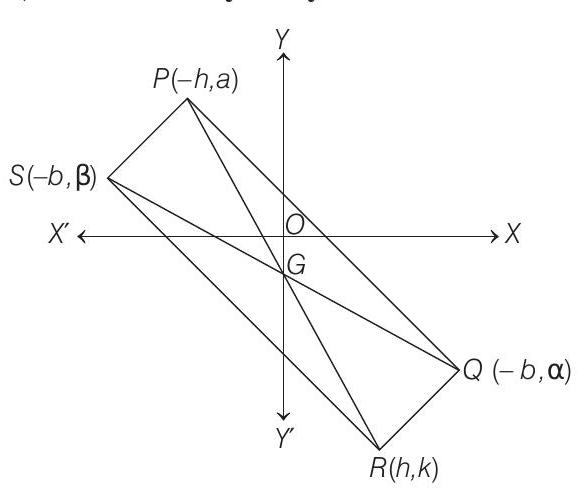
From Eq. (i), we get
$$ \begin{aligned} \alpha-a & =m(b+h) \\ \alpha & =a+m(b+h) \end{aligned} $$
and from Eq. (ii), we get
$$ \begin{aligned} k-\alpha & =-\frac{1}{m}(h-b) \\ \Rightarrow \quad \alpha & =k+\frac{1}{m}(h-b) \end{aligned} $$
From Eqs. (iii) and (iv), we get
$$ \begin{aligned} & a+m(b+h)=k+\frac{1}{m}(h-b) \\ \Rightarrow \quad & a m+m^{2}(b+h)=k m+(h-b) \\ \Rightarrow \quad & \left(m^{2}-1\right) h-m k+b\left(m^{2}+1\right)+a m=0 \end{aligned} $$
Hence, the locus of vertex is
$$ \left(m^{2}-1\right) x-m y+b\left(m^{2}+1\right)+a m=0 $$
