Straight Line and Pair of Straight Lines 1 Question 45
45. The orthocentre of the triangle formed by the lines $x+y=1,2 x+3 y=6$ and $4 x-y+4=0$ lies in quadrant number… .
$(1985,2 M)$
Show Answer
Solution:
- Let $H(h, k)$ be orthocentre.
$\Rightarrow \quad($ slope of $A H) \cdot($ slope of $B C)=-1$
$$ \Rightarrow \quad \frac{k-\frac{16}{7}}{h+\frac{3}{7}} \cdot(-1)=-1 $$
$$ \begin{array}{lc} \Rightarrow & k-\frac{16}{7}=h+\frac{3}{7} \\ \Rightarrow & h-k=-\frac{19}{7} \end{array} $$
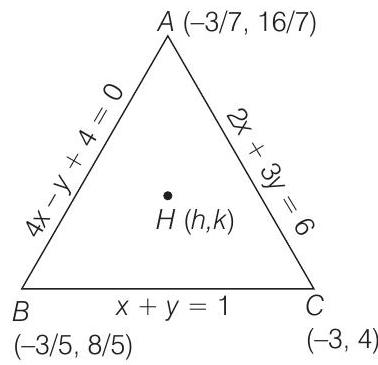
Also, $\quad($ slope of $C H) \cdot($ slope of $A B)=-1$
$$ \begin{aligned} \Rightarrow & & \frac{k-4}{h+3} \cdot(4) & =-1 \\ \Rightarrow & & 4 k-16 & =-h-3 \\ \Rightarrow & & h+4 k & =13 \end{aligned} $$
On solving Eqs. (i) and (ii), we get $h=\frac{3}{7}, k=\frac{22}{7}$
$\therefore \quad$ Orthocentre $\frac{3}{7}, \frac{22}{7}$
Hence, this coordinate lies in the first quadrant.
