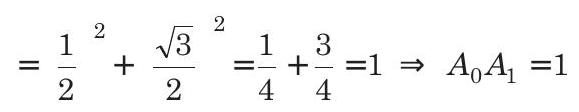Straight Line and Pair of Straight Lines 1 Question 30
30. If $A _0, A _1, A _2, A _3, A _4$ and $A _5$ be a regular hexagon inscribed in a circle of unit radius. Then, the product of the lengths of the line segments $A _0 A _1, A _0 A _2$ and $A _0 A _4$ is
(a) $3 / 4$
(b) $3 \sqrt{3}$
(c) 3
(d) $\frac{3 \sqrt{3}}{2}$
$(1998,2 M)$
Show Answer
Solution:
- Now, $\left(A _0 A _1\right)^{2}=1-\frac{1}{2}^{2}+0-\frac{\sqrt{3}}{2}^{2}$
$$ \begin{aligned} & \quad\left(A _0 A _2\right)^{2}=1+\frac{1}{2}^{2}+0-\frac{\sqrt{3}}{2}^{2} \\ &=\frac{3}{2}^{2}+-\frac{\sqrt{3}}{2}^{2}=\frac{9}{4}+\frac{3}{4}=\frac{12}{4}=3 \\ & \Rightarrow \quad A _0 A _2=\sqrt{3} \\ & \text { and } \quad\left(A _0 A _4\right)^{2}=1+\frac{1}{2}^{2}+0+\frac{\sqrt{3}}{2}^{2} \\ &=\frac{3}{2}^{2}+\frac{3}{4}=\frac{9}{4}+\frac{3}{4}=\frac{12}{4}=3 \\ & \Rightarrow \quad A _0 A _4=\sqrt{3} \\ & \text { Thus, } \quad\left(A _0 A _1\right)\left(A _0 A _2\right)\left(A _0 A _4\right)=3 \end{aligned} $$
